

|
|
| 仧 怘墫悈偺栤戣 偲暦偄偨偩偗偱丂乽偁乕偁丄傗偩側偁両乿偲偨傔懅傪偮偔恖偑偄傞偐傕抦傟傑偣傫丅丂偟偐偟埨怱偟偰偔偩偝偄丅丂偙傟偐傜偍榖偟偡傞偙偲傪拤幚偵庣偭偰偄偗偽丄斾妑揑娙扨偵曽掱幃偑棫偰傜傟傞傛偆偵側傝傑偡丅丂 幚嵺偵傗偭偰傒偨恖偐傜偺儊乕儖偱偡丅 仧偙偺島嵗偺栚師傪彂偄偰偍偒傑偡丅
偙偺儗僢僗儞傪傗傞偺偵昁梫側帪娫偼丂恖偵傛偭偰堘偄傑偡偑丄
偨偭偨偙傟偩偗偺帪娫偱丂怘墫悈偺栤戣丂偑帺怣傪帩偭偰夝偗傞傛偆偵側傞側傜丄傗偭偰傒傞壙抣偼偁傞偲巚偄傑偣傫偐丠丒丒丒偄偐偑偱偡偐丠丒丒丒傗偭偰傒傑偡偐丠 仧偱偼僲乕僩偲昅婰梡嬶傪梡堄偟偰丄偝偭偦偔巒傔傑偟傚偆丅 仸彯丄偙偺島嵗偼丂偍彆偗島嵗廤丂偺僼儕乕乮柍椏乯島嵗偱偡偑丄挊嶌尃偼懚嵼偟傑偡偺偱丄僐僺乕偼偛墦椂偔偩偝偄丅乮挊嶌尃幰丗峳栘怢堦乯 仸偙偺儗僢僗儞偼丄俀侽侾俋擭俋寧偵儕僯儏乕傾儖偟傑偟偨丅丂偦傟偵敽偄丄儕儞僋儈僗傗丄悢帤偺娫堘偄側偳丄弶婜晄椙偑偁傞偐傕偟傟傑偣傫丅婥偑偮偄偨曽偼惀旕偍抦傜偣壓偝偄丅丂仺偙偪傜傊偍婅偄偟傑偡丅 丂側偍丄媽僶乕僕儑儞偼偙偪傜偱偡丅 |
| Copyright (C) since2002 ARAKI, Shin-ichi All Right Reserved. |

儗僢僗儞 侾
|
|
|
| 仠偙偺儗僢僗儞偱偼丂亾偵偮偄偰梋寁側嫲晐怱傪帩偨側偔偰偄偄傛偆偵丂乽亾偵偮偄偰偺怱摼乿丂傪彂偄偰偍偒傑偡丅丂傕偟偁側偨偑 亾丂亖丂傓偢偐偟偄傕偺 偲峫偊偰偄傞偲偟偨傜丄偦傟偼娫堘偄偱偡丅亾丂亖丂乣攞丂偲摨偠傕偺丂丂 偲峫偊偰偔偩偝偄丅丂偙傟偑乽亾偺怱摼乿偱偡丅仠椺偊偽丂俁侽侽墌偺 俀攞偼偄偔傜丠丂偲偄傢傟偨傜偁側偨偼偳偺傛偆偵寁嶼偟傑偡偐丠丂丂摉慠丂師偺傛偆偵傗傝傑偡傛偹丅 俁侽侽墌丂亊丂俀丂 偱偟傚丠丂偱偼丂俁侽侽墌偺俆亾偼偄偔傜丠丂偲偄傢傟偨傜偳偆偱偡偐丠幚偼丂亾 偵側偭偰傕 慡偔摨偠 側偺偱偡丅丂偄偄偱偡偐丠丂偨偲偊偽丒丒丒 |


| 仠曽掱幃偱怘墫悈偺栤戣傪夝偔偲偒偵昁梫側抦幆偼丄偨偭偨偙傟偩偗偱偡丅丂偱偼丄妋擣偺偨傔偵楙廗傪傗偭偰傒傑偟傚偆丅 仠僲乕僩傪梡堄偟偰壓偝偄丅丂偦偟偰師偺栤戣傪傗偭偰傒偰壓偝偄丅丂傢偐傜側偄栤戣偼偲偽偟偰峔偄傑偣傫偑丄摎崌傢偣偺帪偵偟偭偐傝妋擣偟偰偔偩偝偄丅 摎崌傢偣偼亂楙廗亃偛偲偵乮嘆乣嘍偑廔傢偭偨傜乯傗傝傑偡丅丂 偱偼巒傔傑偟傚偆丅 亂楙廗侾亃 嘆丂俁 亾 偼壗攞偺偙偲丠 嘇丂俁係 亾 偼壗攞偺偙偲丠 嘊丂侾俀侽 亾 偼壗攞偺偙偲丠 嘋丂倎 亾 偼壗攞偺偙偲丠 嘍丂乮倎亄倐乯 亾 偼壗攞偺偙偲丠 偱偒傑偟偨偐丠丂偱偼摎崌傢偣傪偟偰壓偝偄丅丂 亂楙廗俀亃師偺栤戣偺乽幃乿偲乽摎乿傪彂偒側偝偄丅 嘆丂俀侽侽 墌 偺 侾侽 亾 偼偄偔傜丠 嘇丂俁侽侽 倗 偺 俉 亾 偼壗倗丠 嘊丂侾俆侽 恖 偺 侾俀侽 亾 偼壗恖丠 嘋丂侾俆侽 恖 偺 倎 亾 偼壗恖丠 嘍丂倷 倗 偺 倶 亾 偼壗倗丠 仠摎崌傢偣傑偱廔傢傝傑偟偨偐丠丂儗僢僗儞侾丂偼偙傟偱廔傢傝偱偡丅丂孞傝曉偟傑偡偑丄拞妛偺曽掱幃偱乽怘墫悈偺栤戣乿傪夝偔偲偒偵昁梫偵側傞丂乽亾偺抦幆乿丂偼偙傟偩偗偱偡丅丂偙傟偩偗傪偟偭偐傝妎偊偰偍偄偰偔偩偝偄丅 |

儗僢僗儞 俀
|
| 仠偙偙偱偼丄怘墫悈偺奊乮恾乯傪昤偔楙廗傪偟傑偡丅丂姷傟傟偽侾暘傕偐偐傝傑偣傫偐傜柺搢偔偝偑傜偢偵傗傝傑偟傚偆丅丂恾傪昤偔偲偒偺億僀儞僩偼丄師偺係偮偱偡丅 |
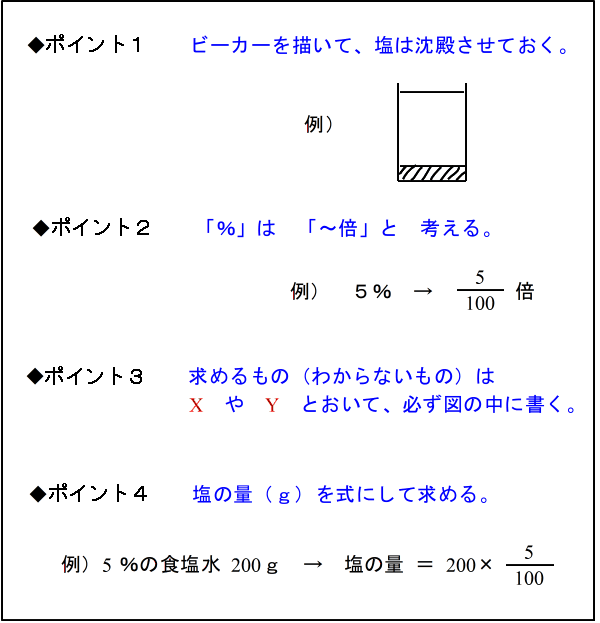
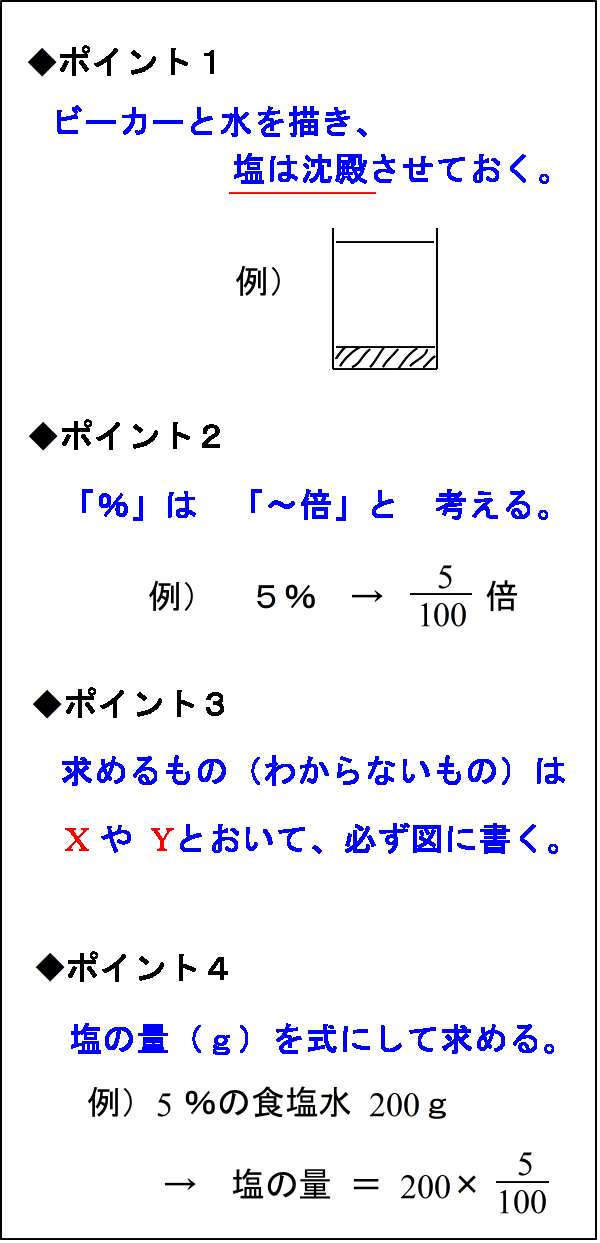
仠偱偼偝偭偦偔楙廗傪偟偰傕傜偄傑偡丅丂傑偢椺戣傪尒偰傕傜偄丄丂偦傟傪尒側偑傜幚嵺偵恾傪昤偄偰傕傜偄傑偡丅丂丂椺戣偼俈偮偁傝丄僷僞乕儞偛偲偵師偺傛偆偵暲傫偱偄傑偡丅丂妎偊側偗傟偽側傜側偄偺偼丂乮侾乯乣乮俆乯偺俆偮偩偗偱偡丅
弨旛塣摦丂A丂B |
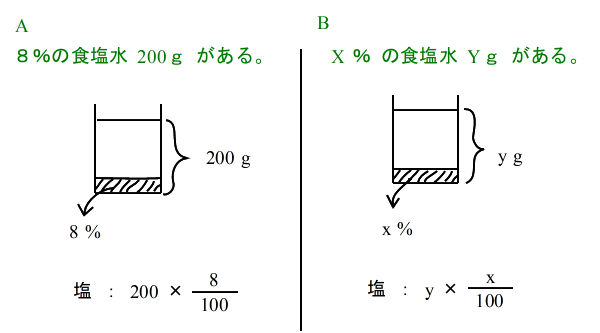
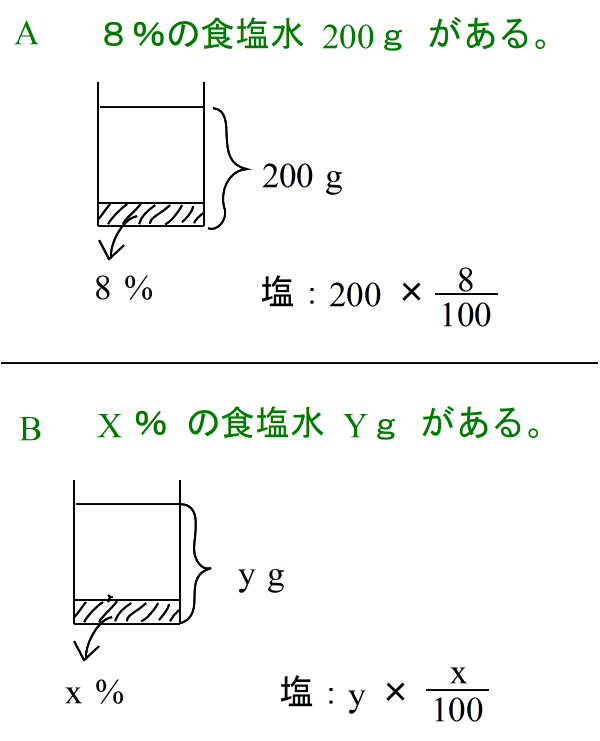
|
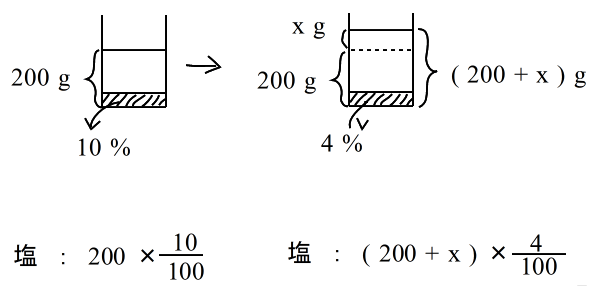
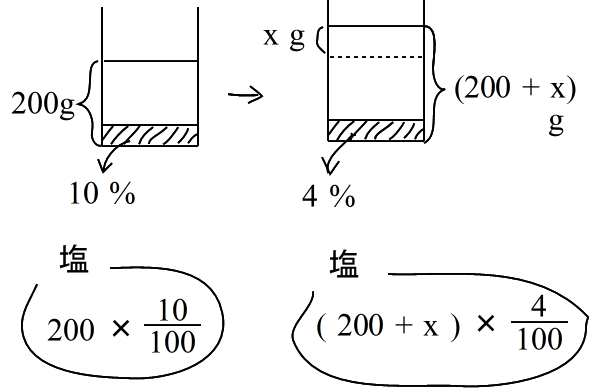
乮侾乯 怘墫悈偵丂悈傪壛偊傞丂 10 亾 偺怘墫悈丂200 g丂偵悈傪丂倶 g 壛偊傞偲丂4 亾 偺怘墫悈偵側傞丅 |
|
仠偱偼丄偙偙偱傑偢弨旛塣摦 A 丄B丂偲丂乮侾乯偺僷僞乕儞丂俁偮偵偮偄偰嶌恾楙廗傪偟偰傕傜偄傑偡丅丂傢偐傜側偔側偭偨傜亂椺戣亃偺奊傪嶲峫偵偟偰峔偄傑偣傫偑丄昁偢帺暘偺庤偱丄僲乕僩偵幚嵺偵奊傪昤偄偰偔偩偝偄丅丂乮摢偺拞偩偗偱峫偊偨傝偟側偄傛偆偵両乯丂偱偼丄巒傔傑偟傚偆丅 亂楙廗俁亃丂師偺偙偲偵拲堄偟偰丄壓偺嘆乣嘊傪恾偵偟側偝偄丅
嘆丂俈亾偺怘墫悈俆侽侽倗傪嶌偭偨丅 嘇丂倎亾偺怘墫悈偑俁侽侽倗偁傞丅 嘊丂係亾偺怘墫悈俀侽侽倗偵悈傪 倷 倗 壛偊偨傜俀亾偺怘墫悈偵側偭偨丅 仠摎崌傢偣傑偱廔傢偭偨傜丄師偺椺戣偵恑傒傑偟傚偆丅 |
|
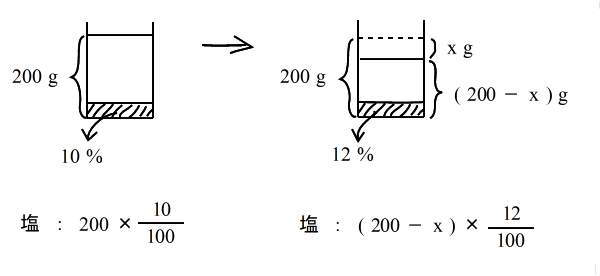
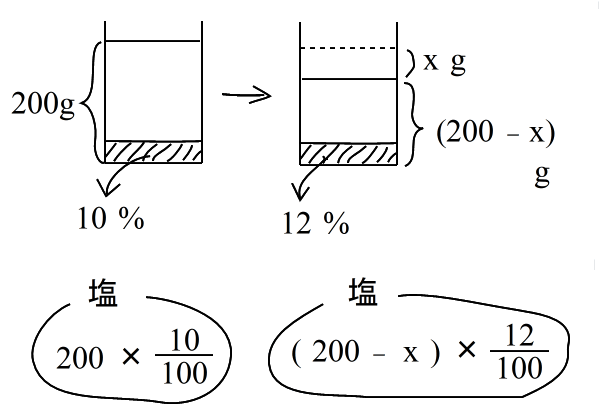
乮俀乯丂怘墫悈偐傜丂悈傪忲敪偝偣傞丂 丂丂10亾 偺怘墫悈 俀侽侽倗 偐傜悈傪 倶倗 忲敪偝偣傞偲 12亾 偺怘墫悈偵側傞丅 |
|
乮俁乯丂怘墫悈偵丂墫傪壛偊傞丂 係亾偺怘墫悈偵 係侽倗 偺怘墫傪壛偊傞偲丄丂侾侽亾偺怘墫悈偵側偭偨丅丂係亾偺怘墫悈偼壗倗偁偭偨偺偐丠 4 亾偺怘墫悈偑丂倶 倗丂偁偭偨偲偟偰 |
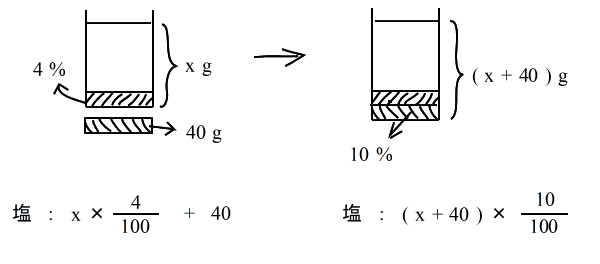
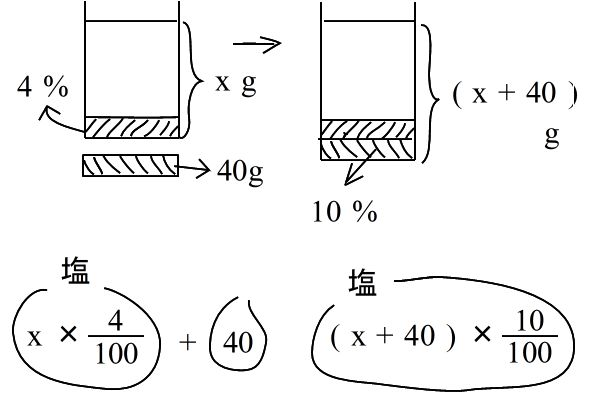
|
仠傑偨丄偙偙偱楙廗傪偟傑偡丅 亂楙廗俁亃丂壓偺拲堄彂偒傪庣偭偰丂嘋丄嘍偺栤戣暥傪恾偵偟側偝偄丅
嘋丂係 亾偺怘墫悈俁侽侽倗偐傜悈傪 x 倗 忲敪偝偣偨傜丂俇亾偺怘墫悈偵側偭偨丅 嘍丂偁傞擹搙偺怘墫悈 300倗 偵丄俀侽倗偺怘墫傪壛偊傞偲丂侾侽亾偺怘墫悈偵側偭偨丅 仠摎崌傢偣傑偱廔傢傝傑偟偨偐丠丂偦傟偱偼師偵堏傝傑偟傚偆丅 |
|
乮係乯丂俀庬椶偺怘墫悈傪崿偤傞丂 仠師偺椺戣偼丄侾擭惗偲俀丄俁擭惗乮楢棫曽掱幃傪廗偭偨恖乯偲偱偼丄恾偺昤偒曽偑彮偟堘偄傑偡丅丂偨偩偟丄俀丄俁擭惗傕侾擭惗梡偺恾偺昤偒曽傪尒偨忋偱丄楢棫梡偺恾偺昤偒曽傪尒偰傒傑偟傚偆丅 10亾偺怘墫悈偲俆亾偺怘墫悈傪崿偤偰丄俉亾偺怘墫悈傪600倗嶌傝偨偄丅 丂偦傟偧傟偺怘墫悈傪壗倗偢偮梡堄偡傟偽傛偄偐丠 仸丂拞妛侾擭梡丂乮侾尦曽掱幃梡乯 10亾偺怘墫悈傪 倶 倗丂偲偡傞偲丄丂丂丂丂 |
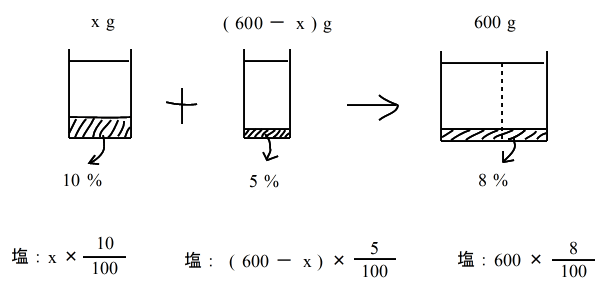
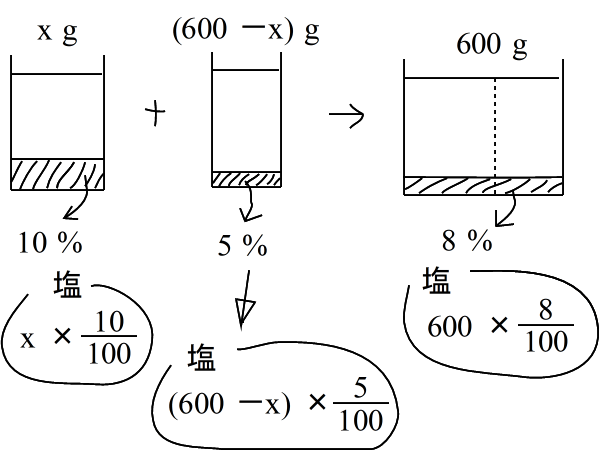
| 丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒 |
| 10亾偺怘墫悈偲俆亾偺怘墫悈傪崿偤偰丄俉亾偺怘墫悈傪600倗嶌傝偨偄丅 丂偦傟偧傟偺怘墫悈傪壗倗偢偮梡堄偡傟偽傛偄偐丠 |
| 仸丂拞妛俀擭梡丂乮楢棫曽掱幃梡乯 10 亾偺傪 x g 丄丂俆亾偺傪 y g丂偲偡傞偲 |
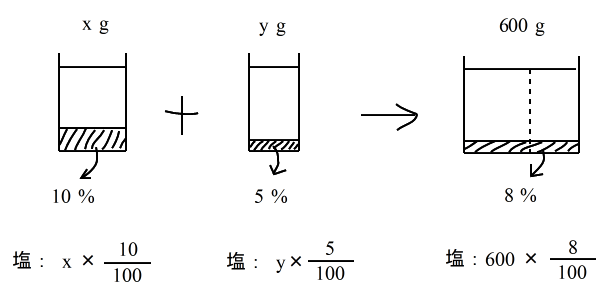
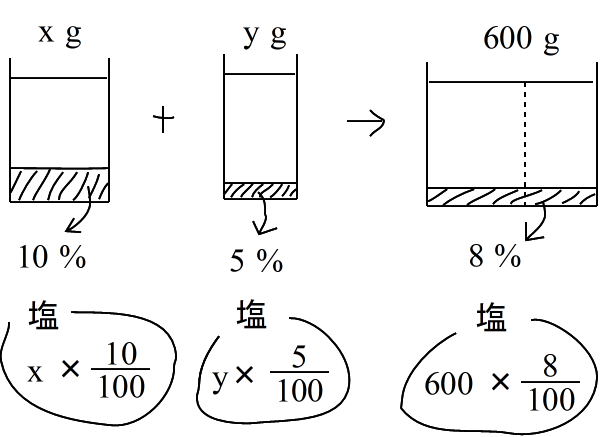
|
乮俆乯丂怘墫悈偐傜丂堦晹暘傪敳偒庢傞丂 |
| 侾侽亾偺怘墫悈 400倗 偑偁傞丅丂偙傟偐傜 倶倗 偺怘墫悈傪庢傝偺偧偒丄丂偐傢傝偵 倶倗 偺悈傪壛偊傞偲丂擹搙偼俇亾偵側偭偨丅 |
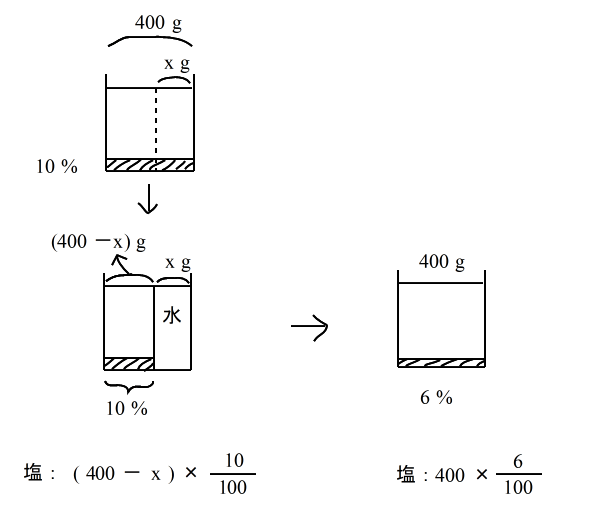
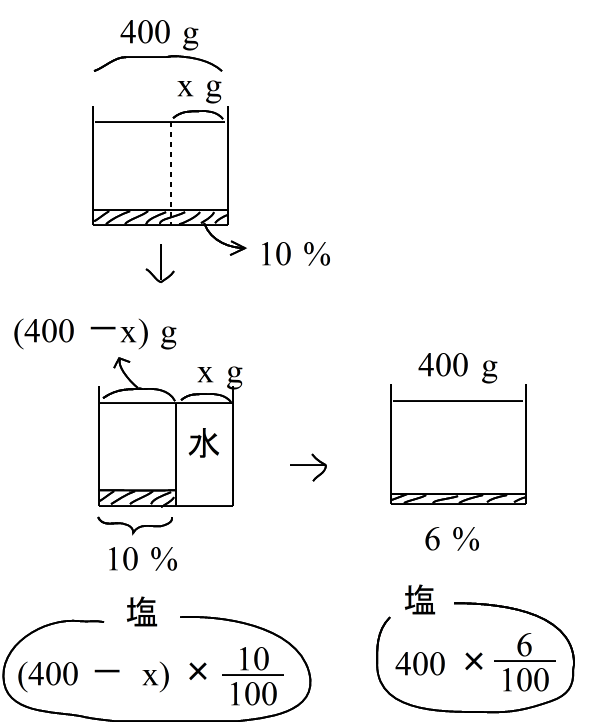
|
|
| 仠偱偼傑偨丄嶌恾楙廗偱偡丅 亂楙廗俁亃丂師偺偙偲偵拲堄偟偰丄壓偺嘐丄嘑傪恾偵偟側偝偄丅
嘐丂俉亾偺怘墫悈偲俁亾偺怘墫悈傪崿偤偨傜丂俇亾偺怘墫悈俆侽侽倗偑偱偒偨丅丂乮壓偺拲堄彂偒傪庣偭偰乯
嘑丂俇亾偺怘墫悈 倶倗 偑偁傞丅丂偙偺偆偪 俀侽侽倗 傪敳偒偲傝丄偐傢傝偵丂俀侽侽倗 偺悈傪壛偊偨傜丂係亾偺怘墫悈偵側偭偨丅 仠偝偰丄摎崌傢偣傑偱廔傢傝傑偟偨偐丠丂偙傟偱儗僢僗儞俀偼廔傢傝偱偡丅丂棟夝偱偒側偐偭偨偲偙傠偼傕偆堦搙尒捈偟偰偐傜丄儗僢僗儞俁偵恑傒傑偟傚偆丅 |

儗僢僗儞俁
|
|
|
| 仠儗僢僗儞俁偱偼丄偄傛偄傛幃傪嶌傞嶌嬈傪傗傝傑偡丅丂偲尵偭偰傕幚偼丄丂儗僢僗儞俀傑偱偵丂傎偲傫偳幃偼姰惉偟偰偄傞偺偱偡丅丂偁偲偼乽亖乮僀僐乕儖乯乿傪偮偗傞偩偗側偺偱偡丅丂偦偺偙偲傪偙傟偐傜愢柧偟傑偡丅 仠乽怘墫悈偺栤戣乿傪夝偔偲偒丄堦斣偺億僀儞僩偵側傞偺偼丄乽怘墫偺検偼摨偠乿偲偄偆偙偲偱偡丅丂偮傑傝丄 |
| 怘墫偺検丂亖丂怘墫偺検 |
| 偲偄偆摍幃乮曽掱幃乯傪嶌傟偽傛偄偺偱偡丅丂偙傟偑丄怘墫悈偺栤戣乮婎慴曇乯傪夝偔偲偒偺嵟戝偺億僀儞僩偲偄偊傑偡丅 仠幚嵺偺椺傪尒偰傒傑偟傚偆丅丂儗僢僗儞俀偱巊偭偨椺戣偺乮侾乯乣乮俆乯傪巚偄弌偟偰偔偩偝偄丅 |
|
|
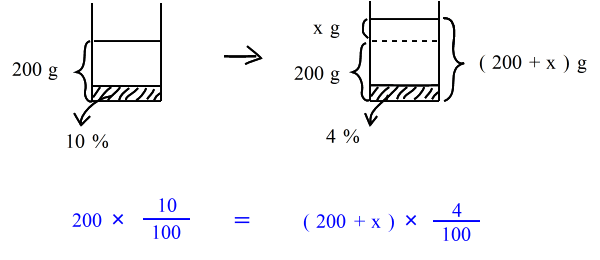
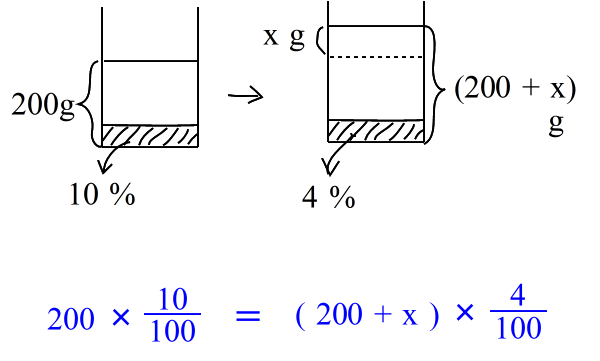
| 乮侾乯丂10亾偺怘墫悈 俀侽侽倗 偵悈傪 倶倗 壛偊傞偲 係亾 偺怘墫悈偵側傞偲偄偆丅丂倶 傪媮傔傛丅 仸恾偲丄怘墫偺幃偼壓偺傛偆側傕偺偱偟偨偹丅 |
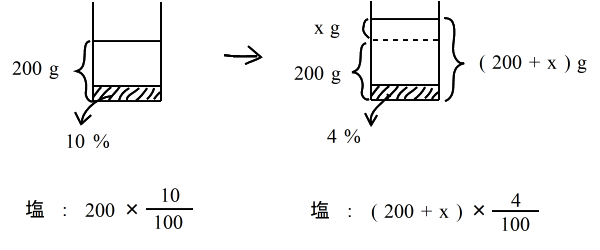

| 偙偙偱拲堄偟偰傎偟偄偺偼丄 |
| 乮嵍偺墫偺検乯丂亖丂乮塃偺墫偺検乯丂 |
| 偲尵偆偙偲偱偡丅丂 丂乮丂悈偺検傗丄擹搙偼曄壔偟偰偄傑偡偑丄墫偺検偼摨偠偱偟傚丠丂乯丂丂偮傑傝丄幃偱昞偡偲丄 |
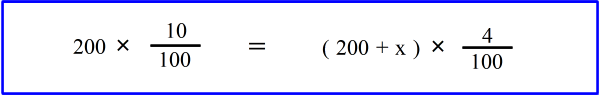
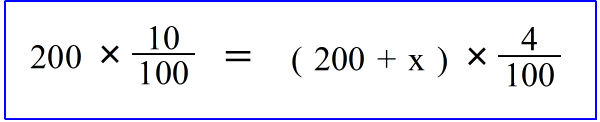
| 偙傟偑丄偙偺栤戣偺曽掱幃偱偡丅丂偙偺曽掱幃傪夝偔偲 丂丂丂倶 亖 300 偲弌偰偒傑偡偐傜丄丂摎偼丂倶 亖 300丂偱廔傢傝丅丂 |
|
|
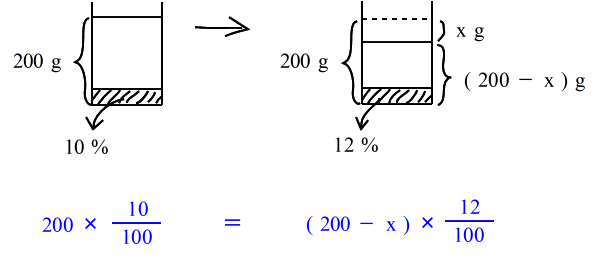
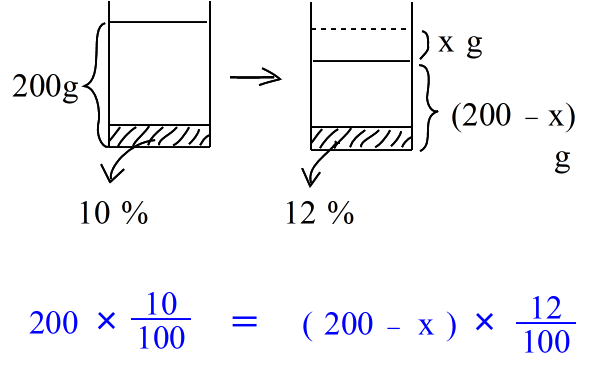
| 乮俀乯丂10亾 偺怘墫悈 俀侽侽倗 偐傜悈傪忲敪偝偣傞偲 12亾 偺怘墫悈偵側偭偨偲偄偆丅丂忲敪偝偣偨悈偺検傪媮傔傛丅丂丂 偲偄偆栤戣偩偭偨傜丄丂偲傝偁偊偢丂倶 倗丂偺悈傪忲敪偝偣傞偲偟偰丄恾偼壓偺傛偆側傕偺偱偟偨丅 |


| 偙偙偱傕摨偠傛偆偵丄 丂乮嵍偺墫偺検乯丂亖丂乮塃偺墫偺検乯丂丂 偱偡偐傜丄 |
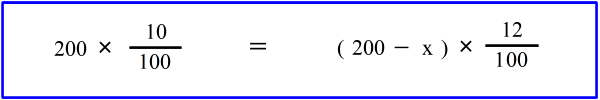
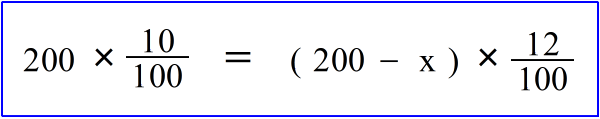
|
|
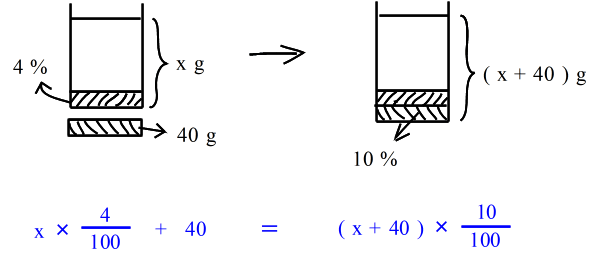
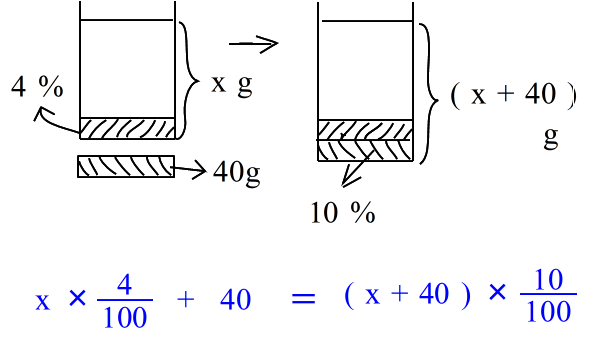
| 乮俁乯丂係亾偺怘墫悈偵 係侽倗 偺怘墫傪壛偊傞偲丄丂侾侽亾偺怘墫悈偵側偭偨丅丂傕偲傕偲係亾偺怘墫悈偼壗倗偁偭偨偺偐丠丂丂 丂係亾偺怘墫悈傪丂倶 倗丂偲偟偰丄 |


| 偙傟傕摨條偵丂嵍偺墫丂亖丂塃偺墫丂丂偩偐傜 |
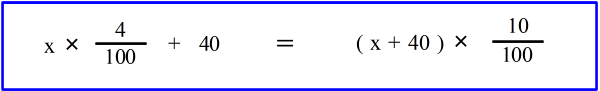
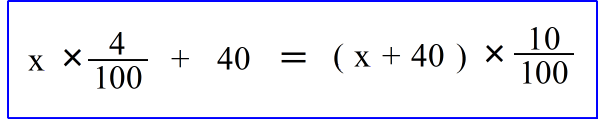
| 偙傟傪夝偄偰丂倶 亖 600丂丂丂丂丂偟偨偑偭偰摎偼丄丂 係亾偺怘墫悈偼丂600 倗丂偲偄偆偙偲偵側傝傑偡丅 |
|
|
| 乮係乯丂10亾偺怘墫悈偲俆亾偺怘墫悈傪崿偤偰丄俉亾偺怘墫悈傪600倗嶌傝偨偄丅 丂偦傟偧傟偺怘墫悈傪壗倗偢偮梡堄偡傟偽傛偄偐丠 仸偙傟傕丄恾偲幃偼壓偺傛偆偱偟偨偹丅 仠拞侾丆拞俁乮侾尦曽掱幃乯梡 |


| 偙偙偱偼 乮10亾偺墫偺検乯亄乮俆亾偺墫偺検乯亖乮俉亾墫偺検乯 偲峫偊偰丄曽掱幃偼 |
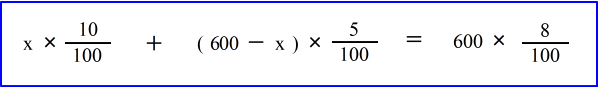
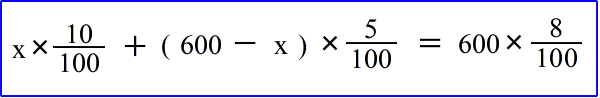
| 偙傟傪夝偔偲丂倶 亖 360丂偲側傝傑偡丅 丂傛偭偰丄 丂10亾偺傪丂360 倗丆丂丂俆亾偺傪丂(600亅360)亖240 倗 偙傟偑摎偲偄偆偙偲偵側傝傑偡丅 |
| 仠拞俀丆拞俁乮楢棫曽掱幃乯梡 10 亾 偺傪 x g , 丂5 亾丂偺傪 y 倗丂偲偡傞 |


| 偙偙偱偼丄 乮10亾偺墫偺検乯亄乮俆亾偺墫偺検乯亖乮俉亾墫偺検乯 偲峫偊丄丂偝傜偵丂乮墫悈偺検乯丂亄丂乮墫悈偺検乯丂亖丂乮墫悈偺検乯 偲偄偆偙偲偐傜丄師偺俀偮偺摍幃偑彂偗傑偡丅 |


| 偙傟傪楢棫偟偰夝偔偲丂倶 亖 360 , 丂倷 亖
240 丂偲側傝傑偡丅 丂傛偭偰 丂10亾偺傪 360倗 丆俆亾偺傪 240倗 偙傟偑摎偲側傝傑偡丅 |
|
|
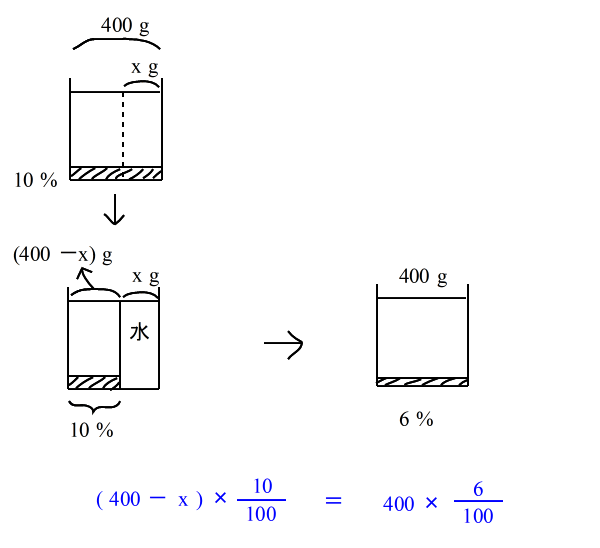
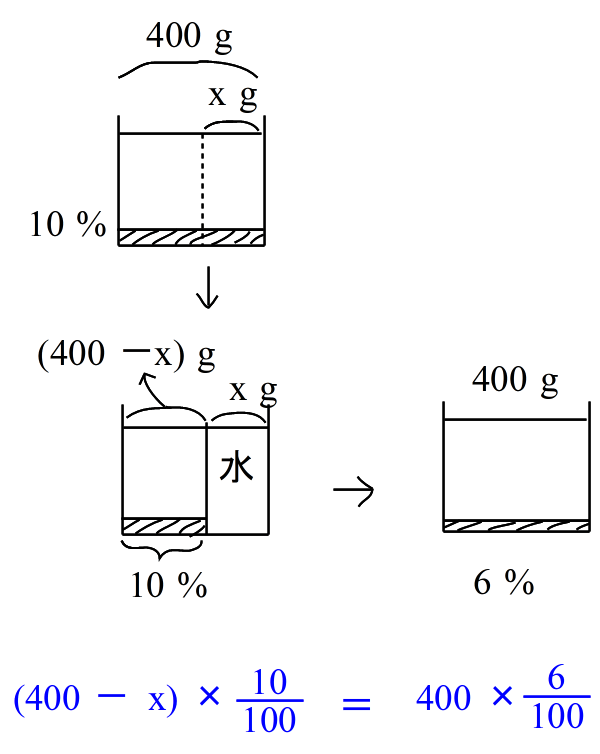
| 乮俆乯丂侾侽亾偺怘墫悈係侽侽倗 偑偁傞丅丂偙傟偐傜 倶倗 偺怘墫悈傪庢傝偺偧偒丄丂偐傢傝偵 倶倗 偺悈傪壛偊傞偲丂擹搙偼俇亾偵側偭偨丅 |


| 偙傟傕摨條偵丂丂墫偺検丂亖丂墫偺検丂丂偲偄偆摍幃傪嶌傟偽丄曽掱幃偺弌棃忋偑傝偱偡丅 仠偝偁丄棟夝偱偒傑偟偨偐丠丂偪傚偭偲偛偪傖偛偪傖偟偰偒傑偟偨偑丄梫偡傞偵丄
亂楙廗係亃丂師偺暥復戣偼丄亂楙廗俁亃偱傗偭偰傕傜偭偨嘆乣嘑偺栤戣偺偆偪丄乮侾乯乣乮俆乯偺俆僷僞乕儞偵摉偨傞丄嘊乣嘑傪丄曽掱幃偺暥復戣偲偟偰傾儗儞僕偟偨傕偺偱偡丅丂偁側偨偺僲乕僩偵昤偄偰偁傞亂楙廗俁亃偺嘊乣嘑偺恾傪尒側偑傜丄曽掱幃傪棫偰丄寁嶼偟丄摎傪弌偟偰偔偩偝偄丅丂乮偨偩偟丄埲慜偵傗偭偨偲偒丄恾偺昤偒曽偑娫堘偭偰偄偨傕偺偼丄夵傔偰昤偒捈偟偰偔偩偝偄丅乯 嘊丂係亾偺怘墫悈俀侽侽倗偵悈傪壛偊偨傜俀亾偺怘墫悈偵側偭偨丅丂壗倗偺悈傪壛偊偨偺偐丠丂悈偺検傪丂倷 倗丂偲偟偰夝偒側偝偄丅 嘋丂係 亾偺怘墫悈俁侽侽倗偐傜悈傪忲敪偝偣偨傜丂俇亾偺怘墫悈偵側偭偨丅丂忲敪偝偣偨悈偺検傪媮傔傛丅 嘍丂偁傞擹搙偺怘墫悈 300倗 偵丄俀侽倗偺怘墫傪壛偊傞偲丂侾侽亾偺怘墫悈偵側偭偨丅丂弶傔偵偁偭偨怘墫悈偺擹搙偼壗亾偐丅 嘐丂俉亾偺怘墫悈偲俁亾偺怘墫悈傪崿偤偨傜丂俇亾偺怘墫悈俆侽侽倗偑偱偒偨丅丂偦傟偧傟壗 倗 偢偮偺怘墫悈偑偁偭偨偺偐丠丂乮壓偺拲堄彂偒傪庣偭偰乯
仠偄偐偑偱偡偐丠丂曽掱幃傪棫偰傞嶌嬈偼偦傟傎偳擄偟偔側偄偱偟傚丠丂恾偝偊昤偄偰偁傟偽偹両丂丂偮傑傝暥復戣傪夝偔嶌嬈偲偄偆偺偼丄幃傪棫偰傞偙偲偑儊僀儞偱偼側偔偰丄乽恾傪昤偔偙偲偑儊僀儞乿偩偲峫偊偰偔偩偝偄丅丂偙傟偼乽怘墫悈偺栤戣乿偵尷偭偨偙偲偱偼偁傝傑偣傫丅 仠偝偁丄偦傟偱偼儗僢僗儞俁偼偙傟偱廔傢傝傑偡丅丂旀傟偨恖偼偪傚偭偲偍媥傒傪庢傝傑偟傚偆丅丂乽傑偩傑偩戝忎晇両乿偲偄偆恖偼丄懕偗偰儗僢僗儞係偵恑傫偱偔偩偝偄丅 拲堄丗拞妛俁擭惗偺奆偝傫傊 拞俁偵側傞偲丄俀師曽掱幃偺暥復戣丂偲偟偰怘墫悈偺栤戣偑弌傞応崌偑偨傑偵偁傝傑偡丅丂偙偺偲偒丄乮俆乯怘墫悈偺堦晹傪敳偒庢傞嶌嬈丂傪俀夞孞傝曉偡偙偲偑懡偄偺偱偡偑丄偙偺応崌偼怘墫偺検傪寁嶼偡傞幃偺棫偰曽傪彮偟曄偊傞昁梫偑偁傝傑偡丅丂乮嶌恾曽朄偼摨偠偱偡丅乯丂丂偙偺偙偲偵偮偄偰偼丄丂婎慴曇偑廔傢偭偰偐傜丄墳梡曇偲偟偰夝愢傪嶌偭偰偁傝傑偡偺偱丄丂傑偢偼婎慴曇傪廔椆偟偰壓偝偄丅 |

儗僢僗儞 係
|
|
|
| 仠偄傛偄傛嵟屻偺儗僢僗儞偵側傝傑偟偨丅丂偙偙偱偼帺椡偱栤戣傪夝偄偰傕傜偄傑偡丅丂孞傝曉偟偵側傝傑偡偑丄丂妎偊側偗傟偽側傜側偄僷僞乕儞偼傢偢偐俆偮偱偟偨偹丅丂 乮侾乯丂悈傪壛偊傞 乮俀乯丂悈傪忲敪偝偣傞 乮俁乯丂墫傪壛偊傞 乮係乯丂俀庬椶偺怘墫悈傪崿偤傞 乮俆乯丂堦晹暘傪敳偒庢傞 憤暅廗偺堄枴偱丄偦偺俆偮偺僷僞乕儞偺恾偺昤偒曽偲曽掱幃偺嶌傝曽傪丄壓偵傑偲傔偰偍偒傑偡偐傜丄偞偭偲栚傪捠偟偰丄亂楙廗俆亃偵恑傫偱偔偩偝偄丅 |
|
乮侾乯丂悈傪壛偊傞丂 |
|
乮俀乯丂悈傪忲敪偝偣傞丂 |
|
乮俁乯丂墫傪壛偊傞丂 |
|
乮係乯丂俀庬椶偺怘墫悈傪崿偤傞 |
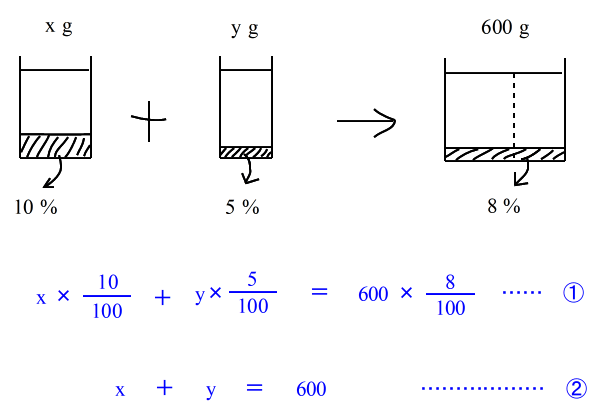
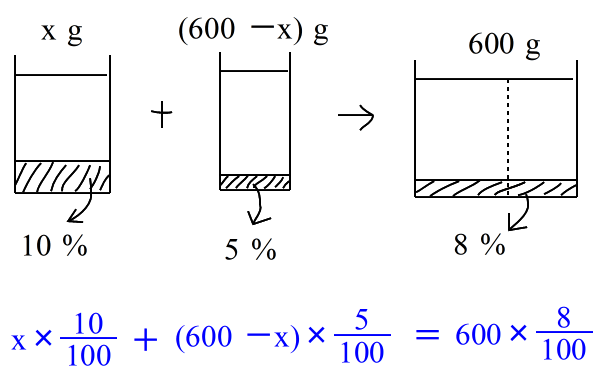
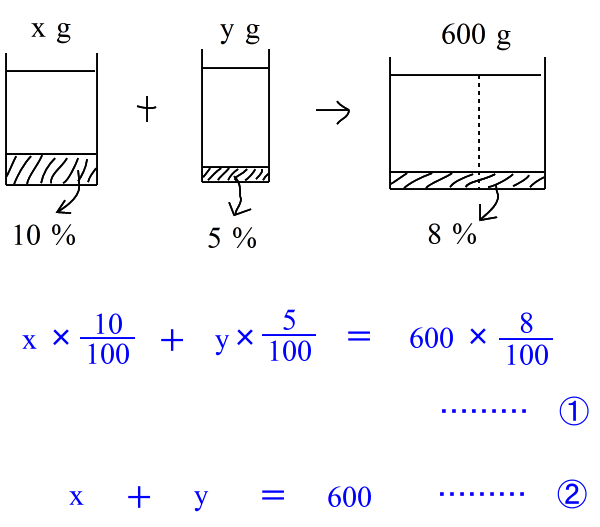
|
乮俆乯丂堦晹暘傪敳偒庢傞 |
|
|
| 亂楙廗俆亃丂師偺栤戣傪撉傒丄恾傪昤偒丄幃傪偨偰丄寁嶼偟丄摎傪弌偟側偝偄丅 嘆丂擹搙 侾俀亾 偺怘墫悈偵悈傪 俀侽侽 倗 壛偊偰丄俉亾偺怘墫悈偵偟偨偄丅丂侾俀亾偺怘墫悈傪壗倗梡堄偡傟偽傛偄偐丠 嘇丂俉亾偺怘墫悈俙偲丂侾俆亾偺怘墫悈俛傪崿偤偰丄侾侽亾偺怘墫悈傪俈侽侽倗嶌傝偨偄丅丂俙丆俛傪偦傟偧傟壗倗偢偮崿偤傟偽傛偄偐丠 嘊丂俉亾偺怘墫悈侾俆侽倗偑偁傞丅丂偙傟傪擬偟偰悈暘傪忲敪偝偣丄侾侽亾偺怘墫悈傪嶌傝偨偄丅丂悈傪壗倗忲敪偝偣傟偽傛偄偐丠丂 嘋丂摵傪娷傓崌嬥偑俀庬椶偁傞丅丂俙偼俋侽亾丄俛偼俇侽亾偺摵傪娷傫偱偄傞丅丂偄傑丄俙丄俛傪梟偐偟崌傢偣偰丂俈侽亾偺摵傪娷傓崌嬥傪係俆倠倗嶌傝偨偄丅丂俙丆俛奺乆壗倠倗偢偮梟偐偣偽傛偄偐丠 嘍丂擹搙俆丏係亾偺怘墫悈偵俆侽倗偺怘墫傪崿偤傞偲丄擹搙偼侾係亾偵側偭偨丅丂俆丏係亾偺怘墫悈偼傕偲傕偲壗倗偁偭偨偺偐丠 嘐丂擹搙侾侽亾偺傾儖僐乕儖悈梟塼俀侽侽倗偑擖偭偨梕婍偑偁傞丅丂偙偺梕婍偐傜 倶 倗 偩偗偔傒弌偟偰丄偐傢傝偵 俀倶 倗 偺悈傪偙偺梕婍偵壛偊偨偲偙傠丄俇亾偺傾儖僐乕儖悈梟塼偵側偭偨丅丂倶偺抣傪媮傔傛丅丂 乮僸儞僩丗傾儖僐乕儖傪墫偺戙傢傝偲偟偰捑揳偝偣偨恾傪昤偔乯 嘑丂乮拞俀丆拞俁梡乯丂俙丆俛俀庬椶偺怘墫悈偑偁傞丅丂俙傪俀侽侽倗丄俛傪係侽侽倗崿偤傞偲俇亾偺怘墫悈偑偱偒丄丂俙傪俁侽侽倗丄俛傪俁侽侽倗崿偤傞偲俆亾偺怘墫悈偑偱偒傞丅丂俙丆俛偺擹搙偼奺乆偄偔傜偐丠 仸丂埲忋偺栤戣偑帺椡偱夝偗傟偽丄岞棫拞妛偺掕婜僥僗僩偲岞棫崅峑偺擖帋栤戣偼丄傎偲傫偳夝偗傞偲巚偄傑偡丅丂扐偟丄拞偵偼師偺栤戣偺傛偆偵丄傗傗柺搢側栤戣傕懚嵼偟傑偡偺偱丄埨怱偼嬛暔偱偡偑丄偒偪偭偲恾傪昤偄偰幃傪棫偰傟偽昁偢夝偗傑偡偐傜丄梋桾偺偁傞恖偼傗偭偰傒偰壓偝偄丅 嘒乮垽抦導偺擖帋栤戣乯俙丄俛俀庬椶偺怘墫悈偑係侽侽倗偢偮偁傞丅怘墫悈俙偐傜俀侽侽倗丄怘墫悈俛偐傜侾侽侽倗傪偲偭偰崿偤偨傜俉亾偺怘墫悈偑偱偒偨丅丂傑偨丄怘墫悈俛偺巆傝偺俁侽侽倗偵俀侽倗偺怘墫傪崿偤偨傜丄丂怘墫悈俙偲摨偠擹搙偵側偭偨丅丂尦偺怘墫悈俙丆俛偺擹搙偼偦傟偧傟壗亾偐丅 嘓乮崄愳導偺擖帋栤戣乯梕婍俙丄俛偵丄堎側傞擹搙偺怘墫悈偑丂俙偵偼係侽侽倗丄俛偵偼俁侽侽倗擖偭偰偄傞丅丂俙丆俛偐傜偦傟偧傟侾侽侽倗偢偮庢傝弌偟丄傛偔崿偤崌傢偣傞偲丄俆亾偺怘墫悈偵側偭偨丅丂 丂丂師偵俙丆俛偵巆偭偰偄傞怘墫悈傪偡傋偰崿偤崌傢偣丄侾侽侽倗偩偗悈傪忲敪偝偣傞偲丄丂俆丏俆亾偺怘墫悈偵側偭偨丅丂 丂丂丂偼偠傔梕婍俙丆俛偵擖偭偰偄偨怘墫悈偺擹搙傪偦傟偧傟 倶 亾丄丂倷 亾 偲偡傞偲偒丄丂倶丄倷 偺抣傪媮傔傛丅 仠偙傟偱乽怘墫悈偺栤戣偺夝偒曽乮婎慴曇乯乿偺儗僢僗儞偼廔傢傝偱偡丅丂傕偆偁側偨偼丄嫵壢彂偲栤戣廤乮昗弨儗儀儖乯偵偺偭偰偄傞拞妛俀擭傑偱偺乽怘墫悈偺栤戣乿偼傎偲傫偳夝偗傞傛偆偵側偭偰偄傞偲巚偄傑偡丅丂僂僜偩偲巚偭偨傜丄幚嵺偵傗偭偰傒偰壓偝偄丅丂 仠傑偨拞妛俁擭惗乮崅峑庴尡惗乯偺偨傔偵丄乽俀師曽掱幃傪巊偭偰夝偔怘墫悈偺栤戣乿偺夝偒曽傪丂墳梡曇偲偟偰梡堄偟偰偁傝傑偡丅丂婎慴曇偲恾偺昤偒曽偼慡偔摨偠偱偡丅丂偨偩丄恾偑侾抜偱偼側偔丄俀抜丄俁抜偵側偭偨傝丄幃偺嶌傝曽傪彮偟岺晇偡傞昁梫偑弌偰偒傑偡丅丂昁梫側恖偼偳傫偳傫僠儍儗儞僕偟偰傒偰偔偩偝偄丅丂丂仺丂墳梡曇傊 丒丒丒丒丂偍旀傟偝傑偱偟偨丂丒丒丒 丂丂丂丂丂 |
| 仸偙偺儗僢僗儞偵懳偡傞偛堄尒丒偛姶憐傪偍暦偐偣壓偝偄丅 儊乕儖傪偄偨偩偗傞曽偼丂偙偪傜偐傜丂偳偆偧両 |
| 仠偍彆偗島嵗僒僀僩偱偼丄拞妛惗偺偨傔偺條乆側嫵嵽丒島嵗傪採嫙偟偰偄傑偡丅丂偨偲偊偽 側偳偱偡丅丂嫽枴偑偁偭偨傜惀旕偺偧偄偰傒偰偔偩偝偄丅 |
| 偍彆偗島嵗憤崌僒僀僩傊 |
| Copyright (C) 丂since 2002 丂ARAKI, Shin-ichi All Right Reserved. |