

|
ホーム > |
| メネラウスの定理は |
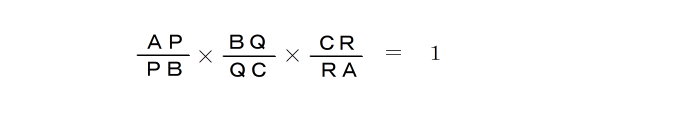
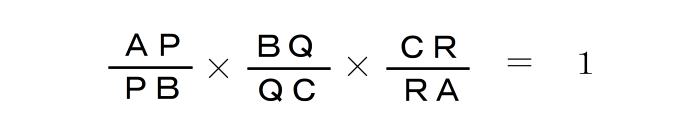
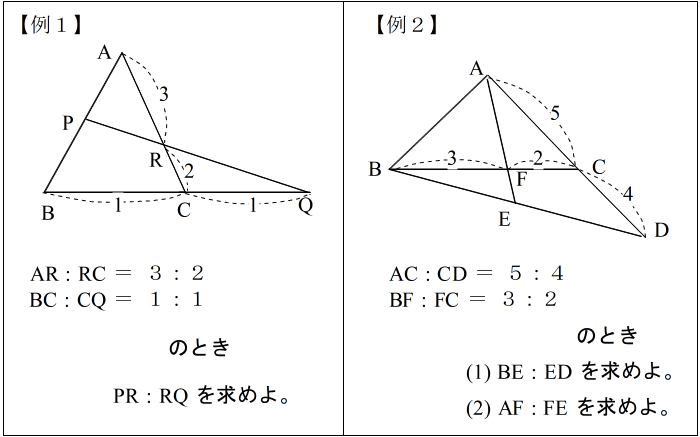
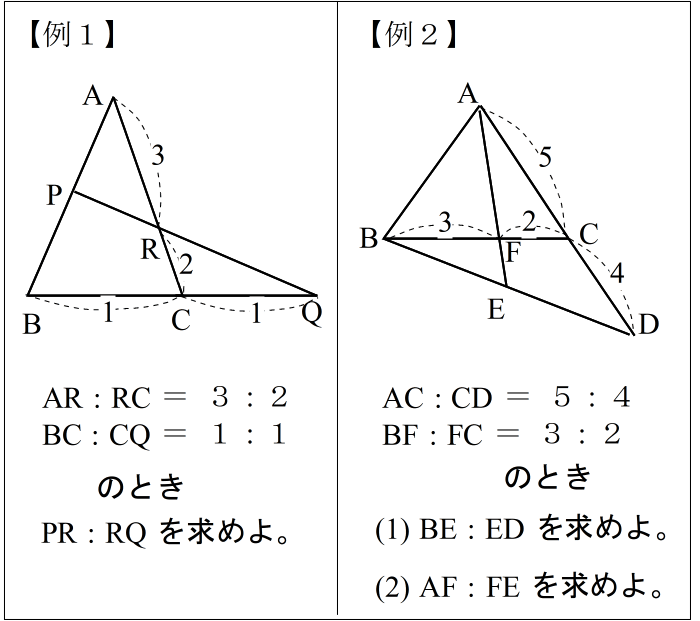
| とかいう公式を覚えても、問題を解くときは あまり使い物になりません。 たとえば次のような問題では、自分で式を作り替えなければなりません。 |
| この講座では、どのような条件で出されても、それがメネラウスで解ける問題かどうかを素早く判断し、素早く立式するためのちょっとしたコツを、お伝えしていこうと思います。 この講座をやるのに必要な時間は メネラウスの定理について ・解説を読むのに5分〜10分 ・練習問題をやるのに 10分〜15分 チェバの定理について ・解説を読むのに5分〜10分 ・練習問題をやるのに 10分〜15分 位だろうと思います。 小一時間後には、メネラウス、チェバについては隣の受験生よりも確実に上の実力をつけているはずです。 では さっそく始めましょう。 【 メネラウスの解法 】 メネラウスの定理は 三角形と その各辺の内分点・外分点を結ぶ直線(線分)との関係を表した式です。 たとえば 公式として使われる下の式は、 △ABC と 線分P−R−Q についてのものです。 |
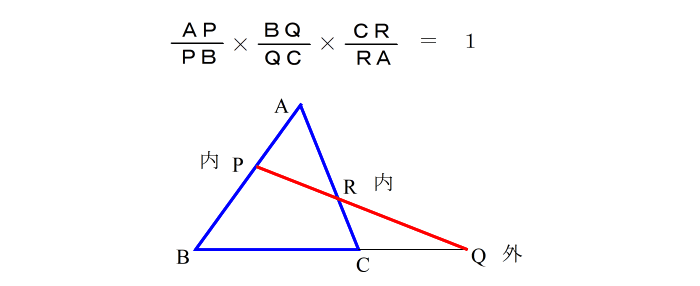
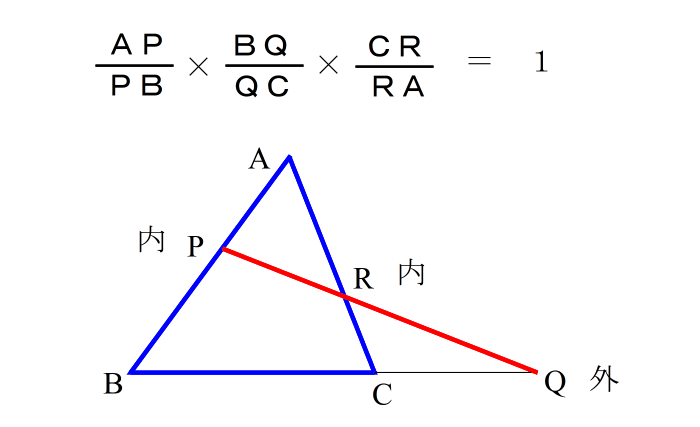
| 従って、メネラウスの定理を使うときは、 ・どの三角形を使うのか ・どの線分を使うのか この2つのことを確定しておかなければなりません。 繰り返しますが、使う線分というのは、 内分点や外分点を結んだもの になっています。 上の例では、 Pは ABの 内分点 Qは BCの 外分点 Rは ACの 内分点 さて、ではこれから次の3つのステップで 問題を解く手順を解説します。 ステップ1: 三角形を見つける ステップ2: 線分を見つける ステップ3: 式を立てる 一見 面倒くさそうですが、実際には 問題文を読んで立式まで1分もかかりません。 では始めましょう。 【ステップ1:三角形を見つける】 |
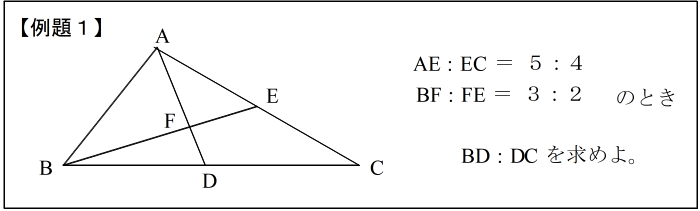
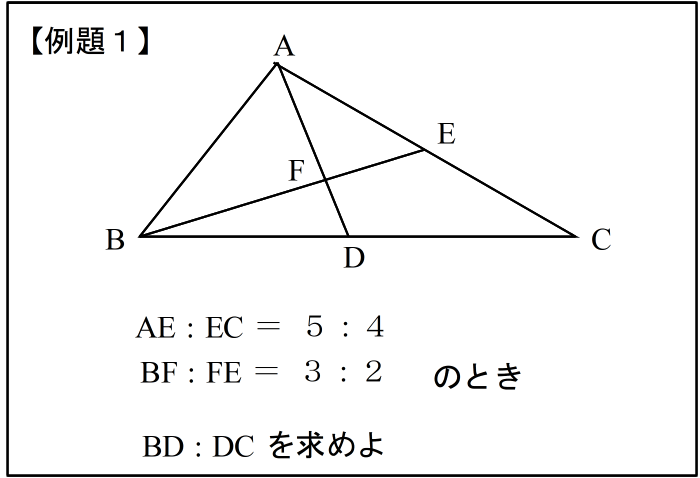
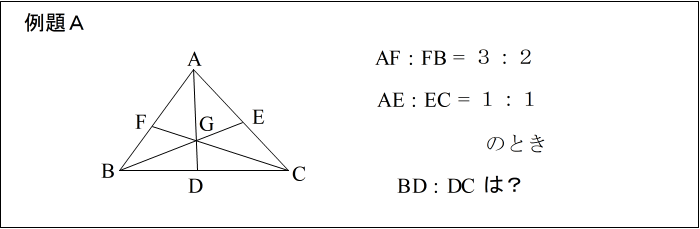
| 手順1: 図を描き、問題文に書いてある条件 AE : EC = 5:4 と BF : FE = 3:2 を図に描き込んで、波線(なみせん)を引く。 |
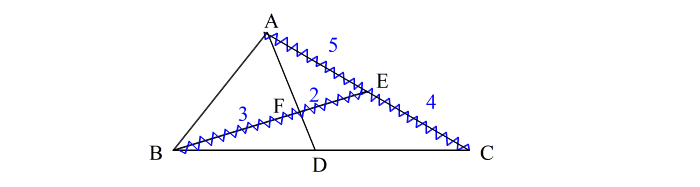
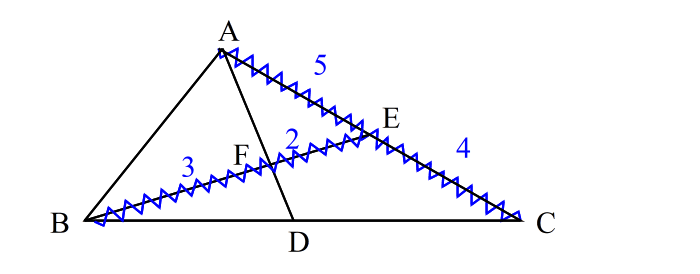
| 手順2: 次に、求める辺の比を x、y とおいて図に書き込み、これにも波線を引く。 |
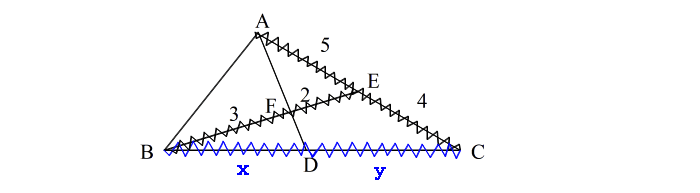
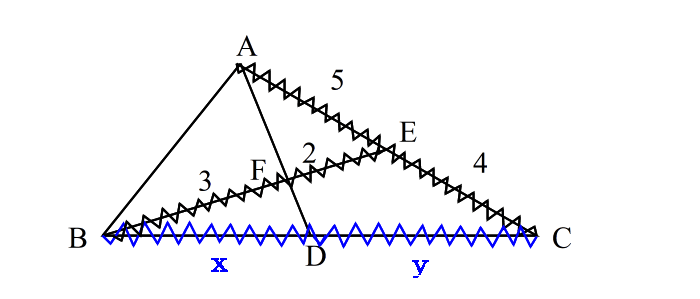
| 手順3: 波線で囲まれた三角形を見つける。 ここでは△EBC。 これが「使う三角形」です。 |
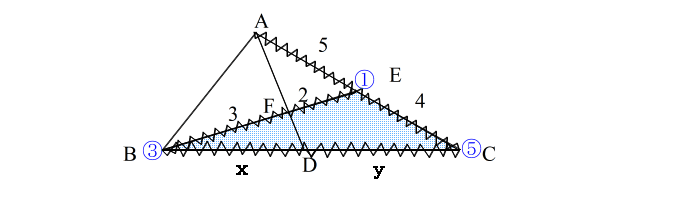
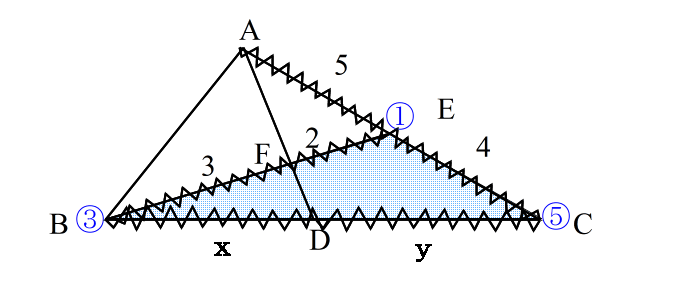
| 手順4: 三角形の頂点を ①、 ③、 ⑤ とおく (どこの頂点を①にとっても良い。) 【ステップ2:線分を見つける】 手順5: 辺①③の 内(外)分点を②とする。 |
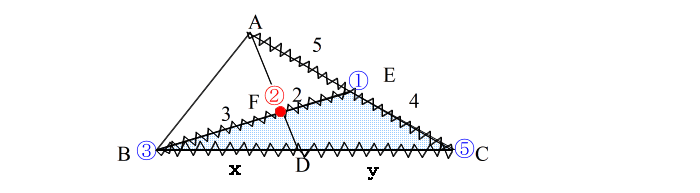
| 同様に 辺③⑤の 内(外)分点を④ 辺⑤①の 内(外)分点を⑥ とする。 |
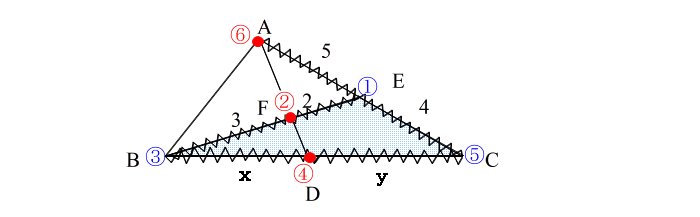
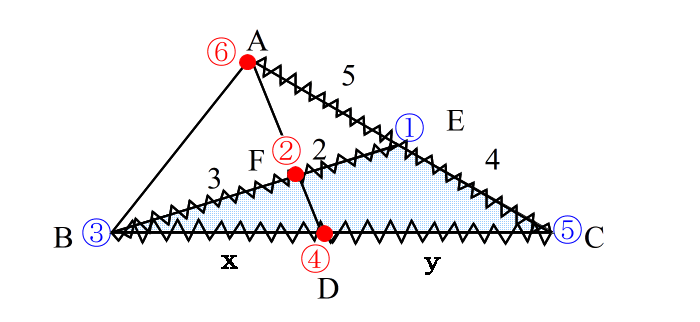
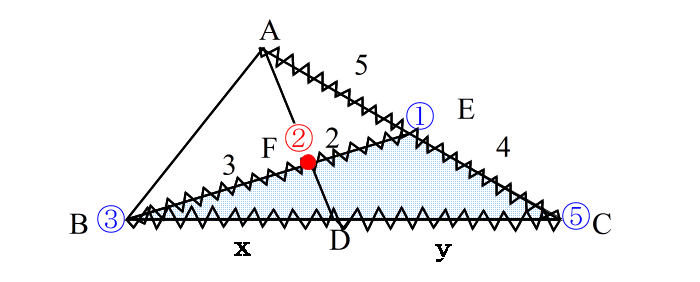
| 手順6: ②−④−⑥ が一直線になっていれば メネラウスを使えると判断する。 注意:ここで一番注意すべき事は 番号の組み合わせを間違えないこと! ① ③ → ② ③ ⑤ → ④ ⑤ ① → ⑥ これでないといけません。 【ステップ3:式を立てる】 さて、いよいよ立式に移りますが、その前に次の数字の列を 声を出して2回読んで下さい。 ①②・②③・③④・④⑤・⑤⑥・⑥① 2回 読みましたか。 さて・・・・ メネラウスの定理の公式を、上の数字で表すと |

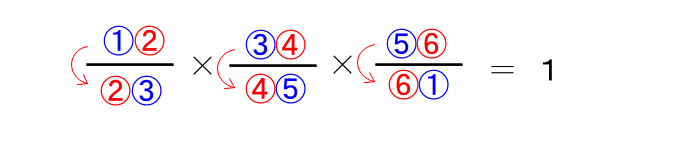
| となります。 このように数字の順番に従って立式していけば、自然とメネラウスの公式にたどり着けます。 先ほどの例題で言うと |
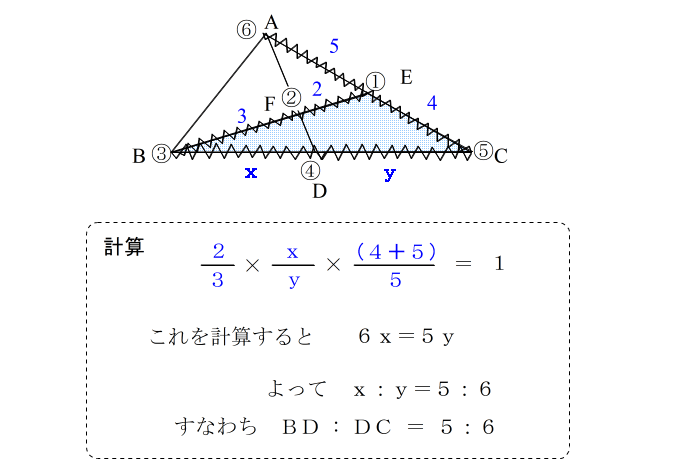
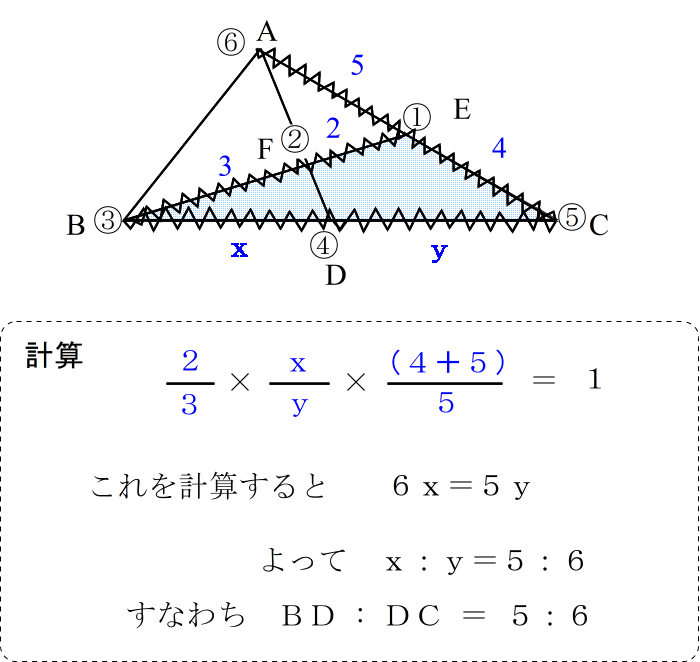
| 正式な答案としては |
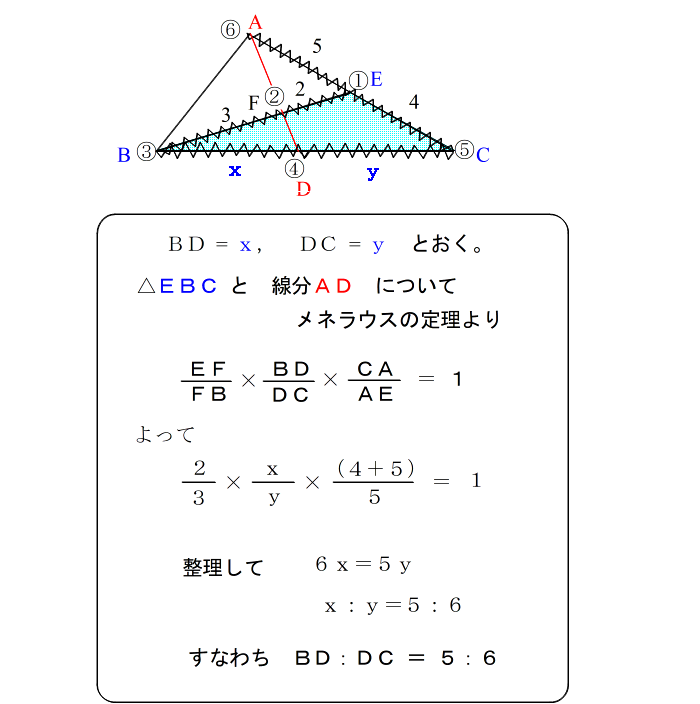

| では、もう一問解いてみましょう。 |
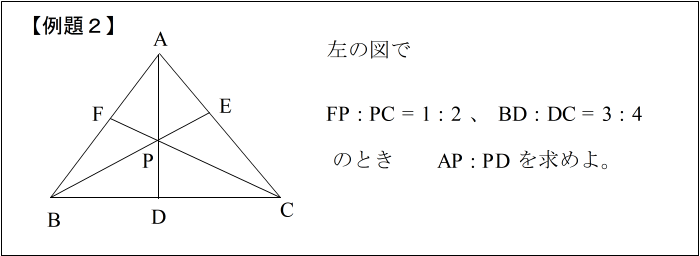
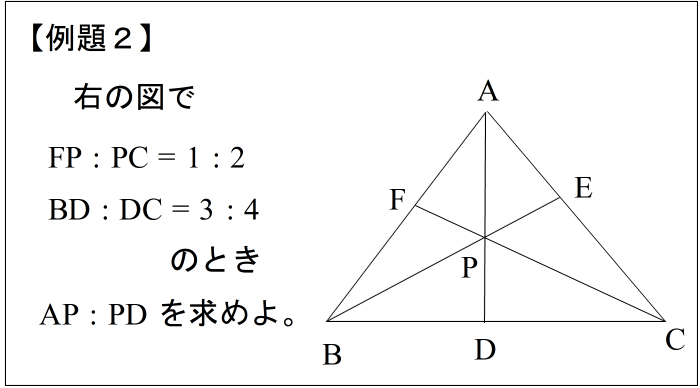
| まず三角形を見つけましょう。 条件のFP : PC, BD : DC の比を書いて波線 AP , PD をそれぞれ x,y とおいて波線 すると 下のような図になります。 |
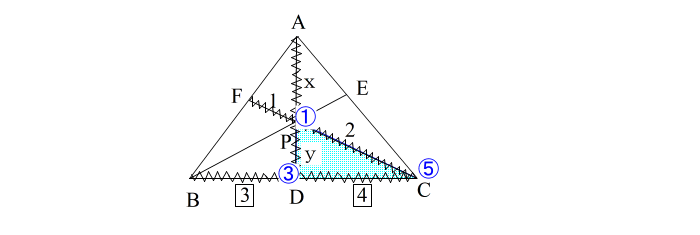
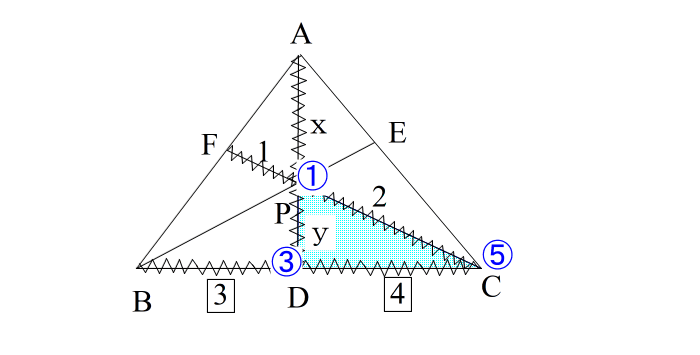
| → 使う三角形は △PDC とわかる。 → 頂点に ①、③、⑤ をふって → 各辺の内外分点を探し、 ①③ の分点 → ② ③⑤ の分点 → ④ ⑤① の分点 → ⑥ と番号を振る。 |
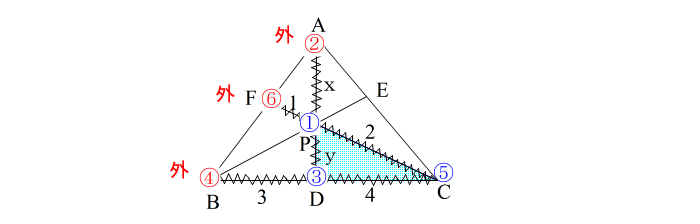
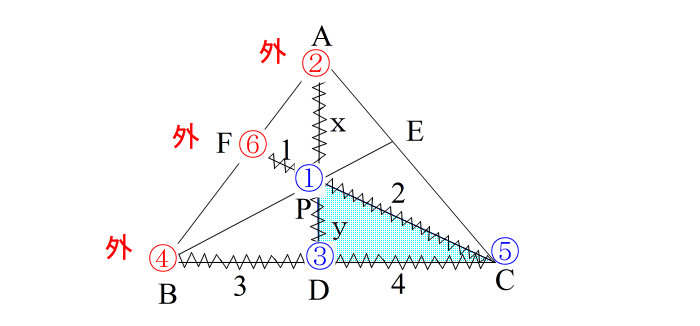
| → ②④⑥が一直線であることを確認 この問題は 3つとも 外分点 ですが大丈夫です。 こういう場合もメネラウスは使えます。 とにかく、②④⑥が一直線であること これが最も重要なことです。 |
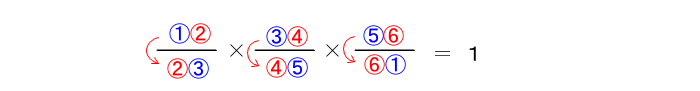

| に当てはめて 立式 |
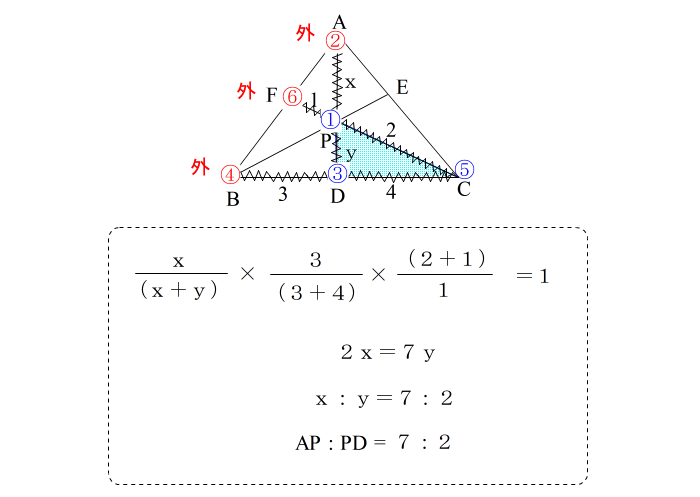
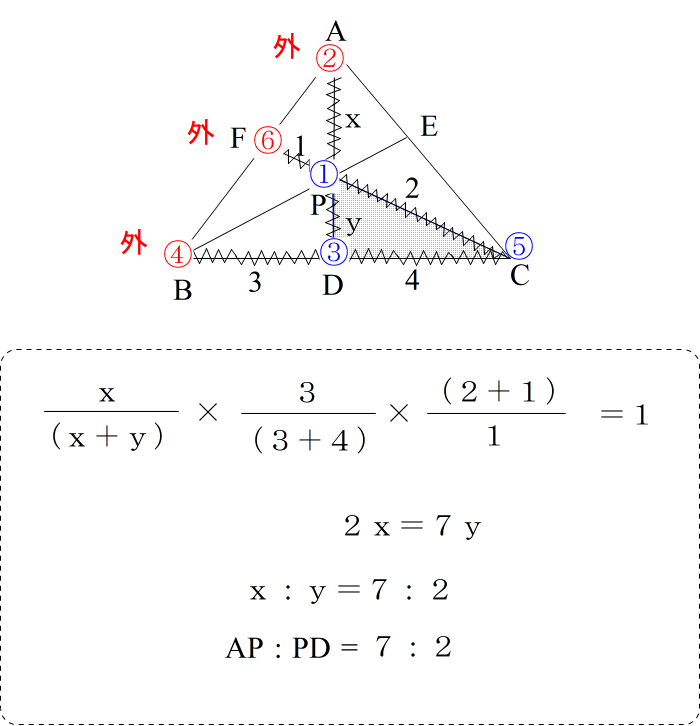
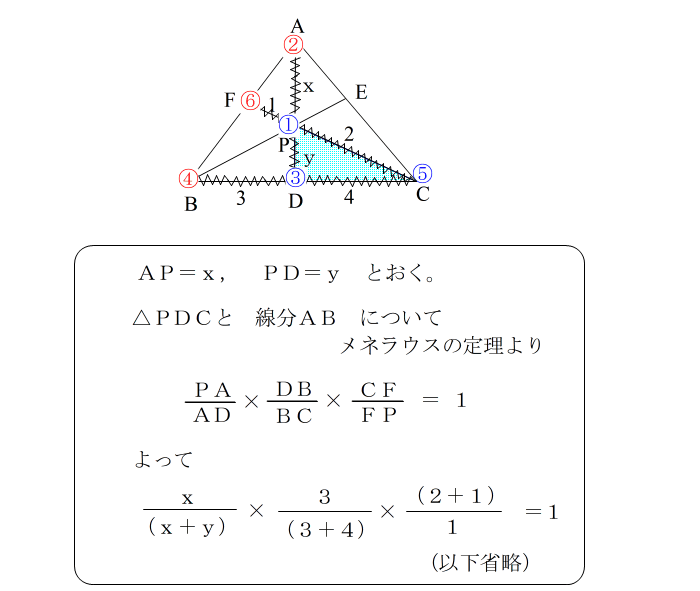
| 正式な答案としては |
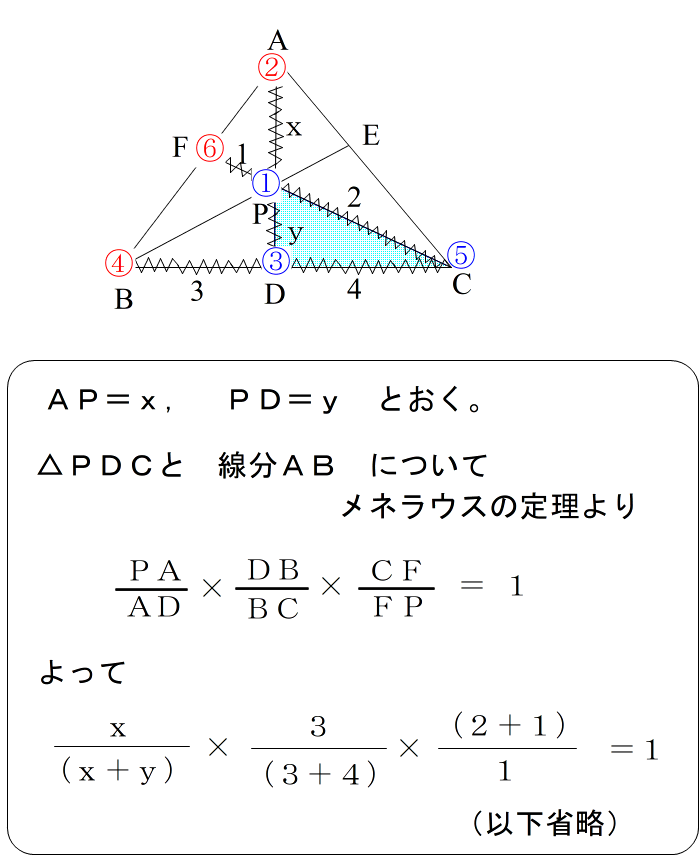
| 今回は外分点3つを使うパターンでしたが、 メネラウスには 2つのパターンしかありません。 ・内分点2つと 外分点1つの場合 ・外分点 3つの場合 図形的なイメージは 下図のようになります。 |
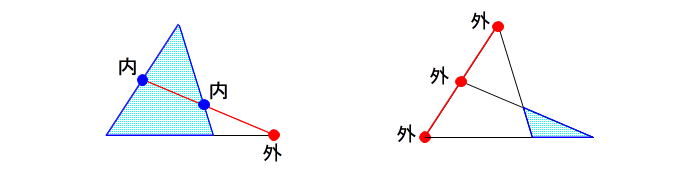
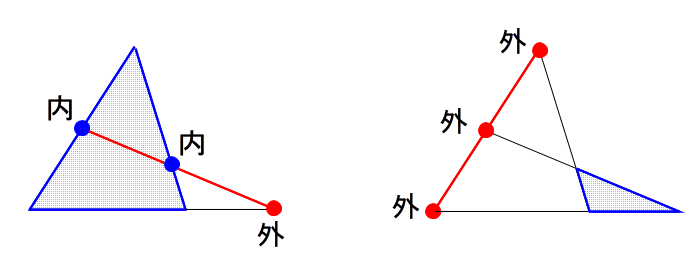
| 学校の初級の問題では 内・内・外が多いですが 外・外・外もいつでも使えるようにしておかないと メネラウスのマスターにはなれません。 【手順のまとめ】 (1)与えられた条件、求める辺に波線を引く。 (2)波線で囲まれた三角形を見つけ→①③⑤ (3)各辺の分点を見つけ → ②④⑥ 注:①③→②、 ③⑤→④、⑤①→⑥ を厳守 (4)②−④−⑥が直線ならメネラウスが使える。 (5) ①②・②③・③④・・・=1 で立式 では実際に問題を4問ほど 解いてみて下さい。 今までの手順をたどれば、あっ!という間に答が出るはずです。 |
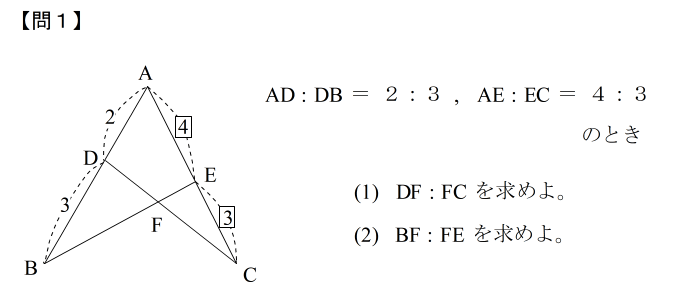
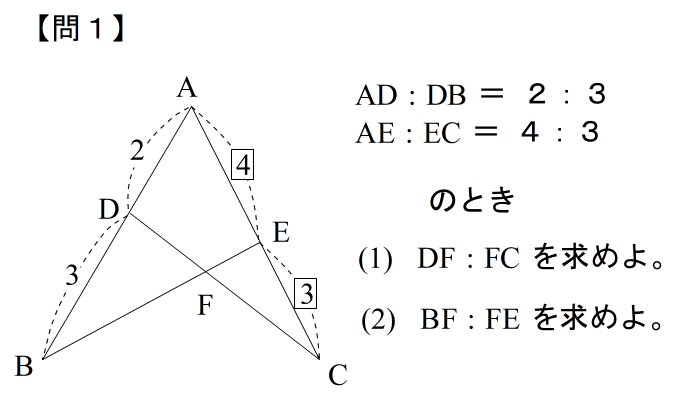
| 答えはこちら |
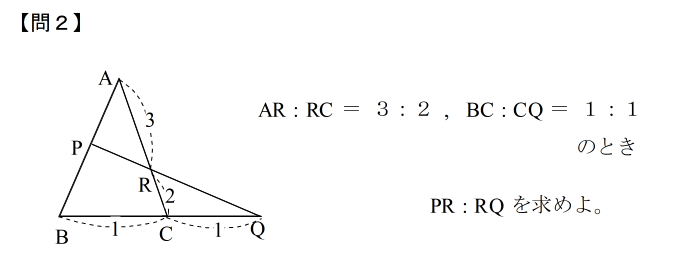
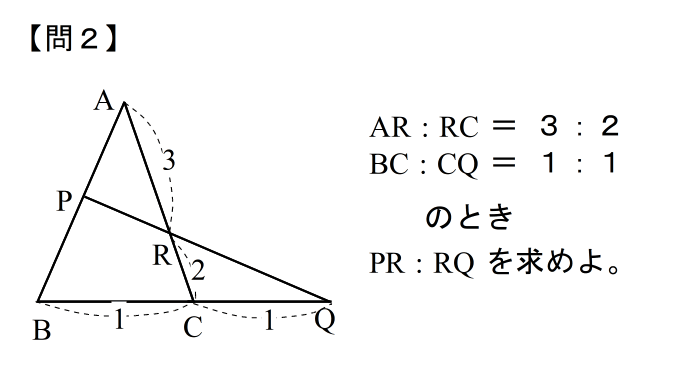
| 答えはこちら |
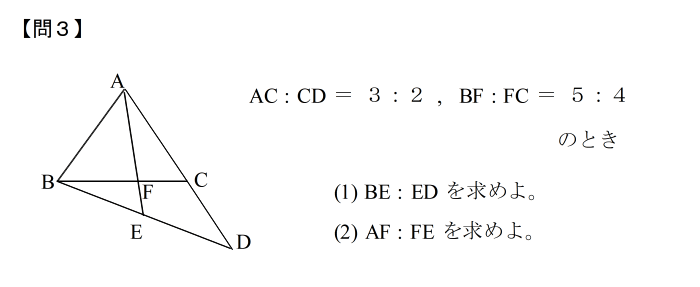
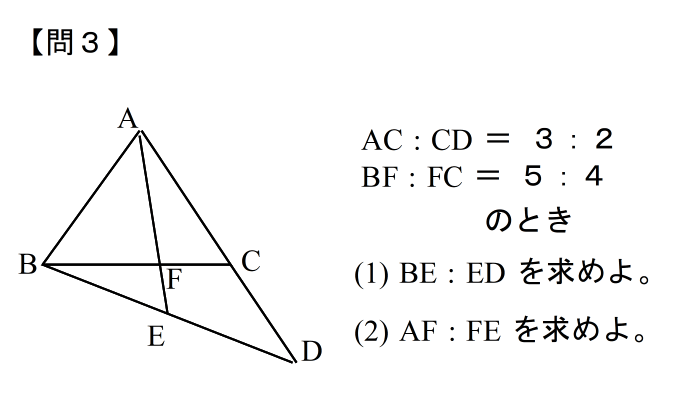
| 答えはこちら |
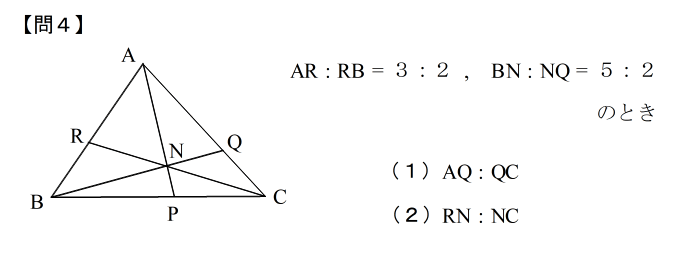
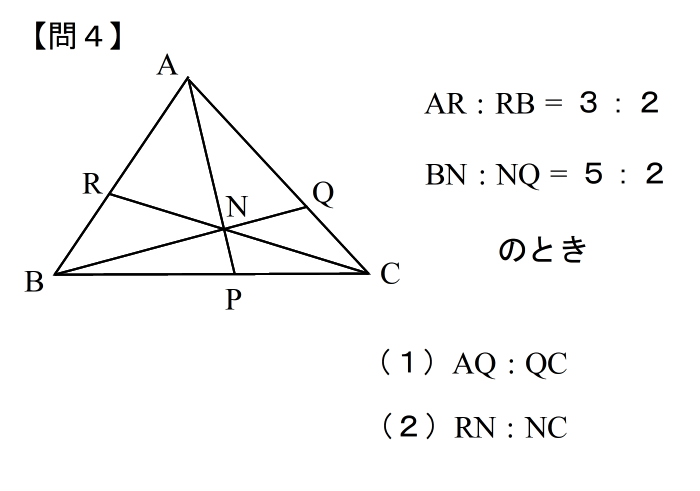
| 答えはこちら |
|
これでメネラウスの定理についての講座は終わりです。 ご自分の問題集に戻って、問題を解いてみて下さい。おそらくすらすら解けると思います。 【 チェバの定理の解法 】 メネラウスの定理が使えるようになった人のために、チェバの定理についても同じような解説を作っていますので、興味があったら読んでみて下さい。 メネラウスの説明の中で、②④⑥が直線になったらメネラウスが使える、と言いましたが、では 直線にならなかったらどうするの? という問題が出てきますよね。 そこで登場するのがチェバの定理です。 チェバの定理はメネラウスの定理よりもわかりやすい、と思っている人がいるかもしれませんが、実際にはそうでもありません。 簡単なのは教科書レベルの下のような問題の時だけです。 |
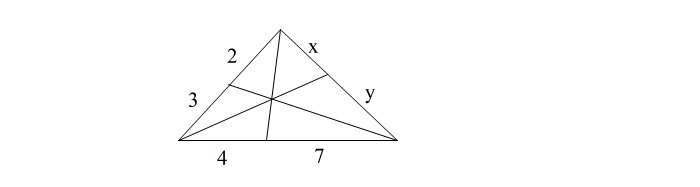
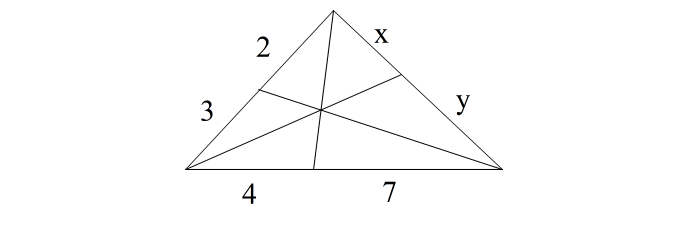
| これが |
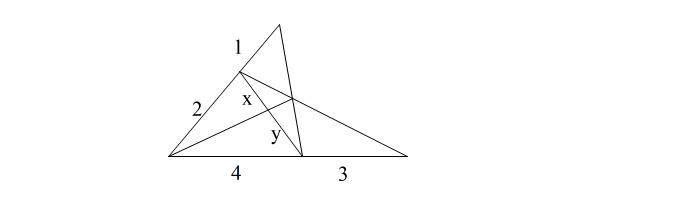
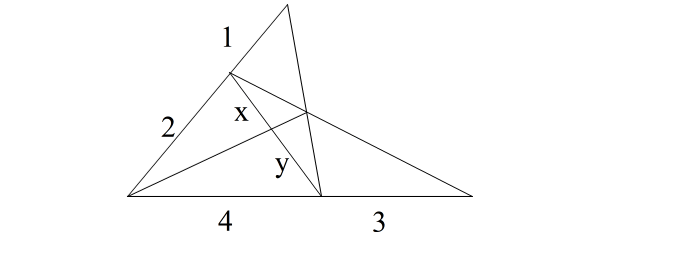
| こんな感じの図になって、?????となったり、 メネラウスかな、と思っていたら解けなくて、答えを見たらチェバだった、みたいな経験はありませんか? これまでにはなくても、これから出会うかもしれませんね。 でも安心して下さい。 前半のメネラウスの定理の手法 (①③⑤−②④⑥システム) をわかっていれば、特に問題なく式は作れるようになります。 立式までの手順はほどんど同じだからです。 では具体的に問題を解きながら説明します。 これから2〜3パターンの問題を紹介しますが、 手順は全て同じ。 しかもその手順の大部分がメネラウスと同じです。 【手順】 (1)問題に関係する辺に波線を引く (2)波線から三角形を確定し ①③⑤とふる (3)辺①③の内外分点を② (3)辺③⑤の内外分点を④ (3)辺⑤①の内外分点を⑥ とする ここまではメネラウスと全く同じ ②④⑥が一直線上に あればメネラウス。 直線上になければ 次の(4)(5)でチェバが使えるか確認します。 (4)頂点①と対辺③⑤の分点④を直線で結ぶ (4)頂点③と対辺⑤①の分点⑥を直線で結ぶ (4)頂点⑤と対辺①③の分点②を直線で結ぶ (5)上の3直線 ①−④、③−⑥、⑤−②が 一点で交わっていればチェバの定理が使えると判断する。 ※(4)(5)がわかりにくいですが、後で 具体的に説明します。 (6)最後に メネラウスと同じ式に当てはめる まず教科書レベルで説明します。 |
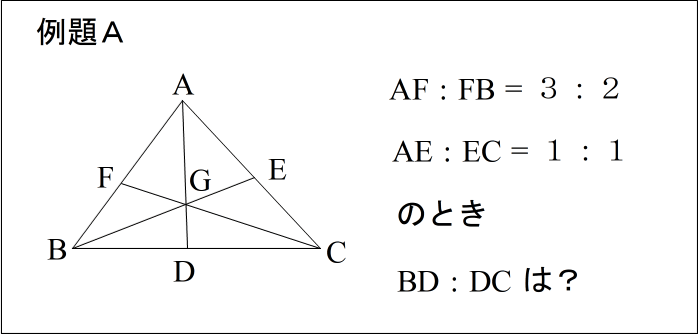
| 作業 (1)問題に関係する辺に波線を引く。 (2)三角形を確定し ①③⑤とふる。 |
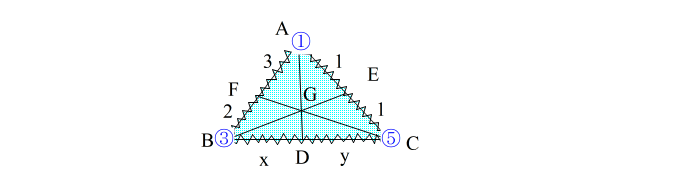
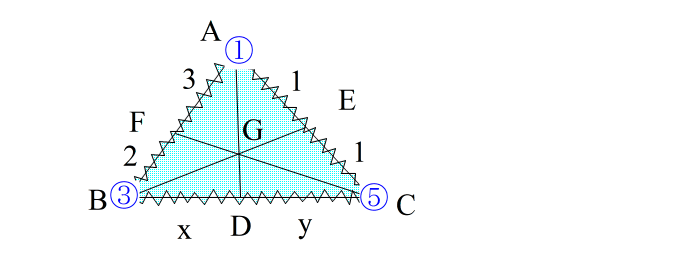
| (3)辺①③の内外分点を② 辺③⑤の内外分点を④ 辺⑤①の内外分点を⑥ とする |
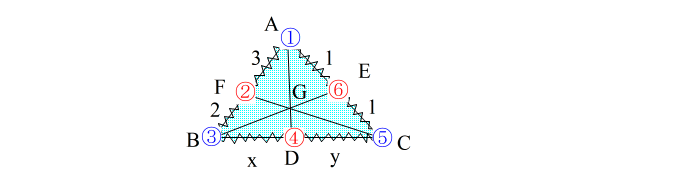
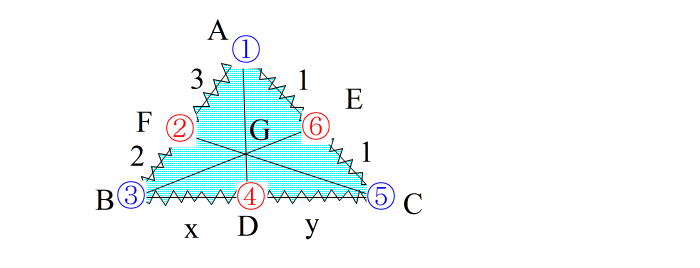
| この段階で、②④⑥が一直線上にないのでメネラウスは使えない、と判断する。 しかしチェバが使えるかもしれないので、次の作業をやる。 (4)頂点①と対辺③⑤の分点④を直線で結ぶ。 |
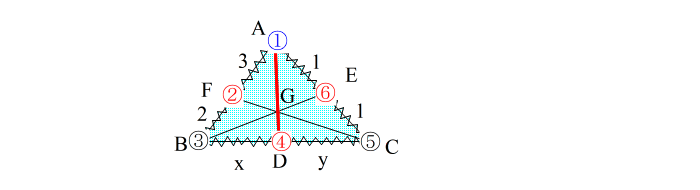
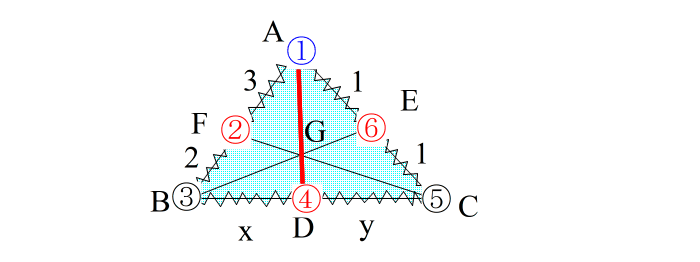
| 同様に 頂点③と対辺⑤①の分点⑥を直線で結ぶ。 頂点⑤と対辺①③の分点②を直線で結ぶ。 |
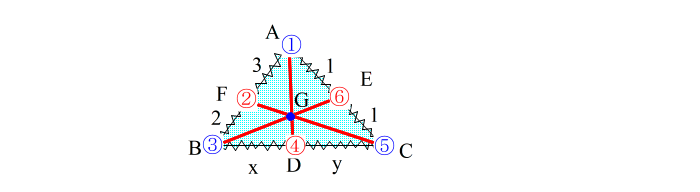
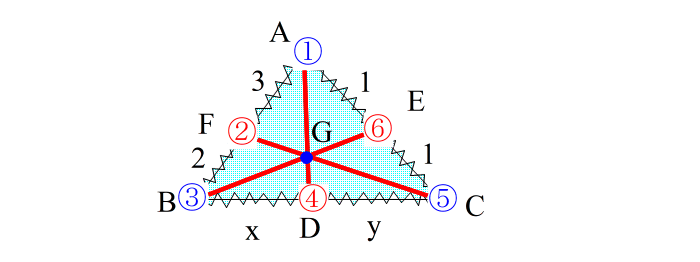
| (5)3直線 ①−④ ③−⑥ ⑤−② が一点で交わっていれば チェバの定理が使える、と判断する。 → 今回は点Gで交わっているのでOK。 この交点を 「 共点 」 といいます。 この共点が存在しないとチェバは使えませんので、下のような図の時は当然ダメです。 |
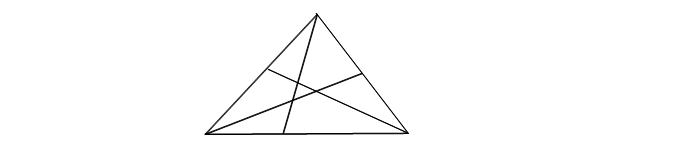
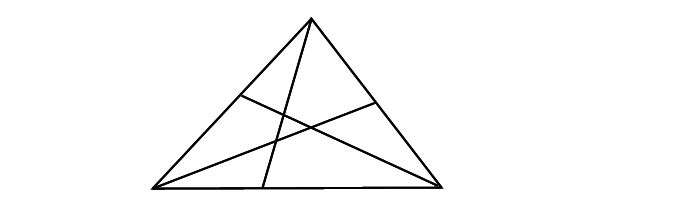
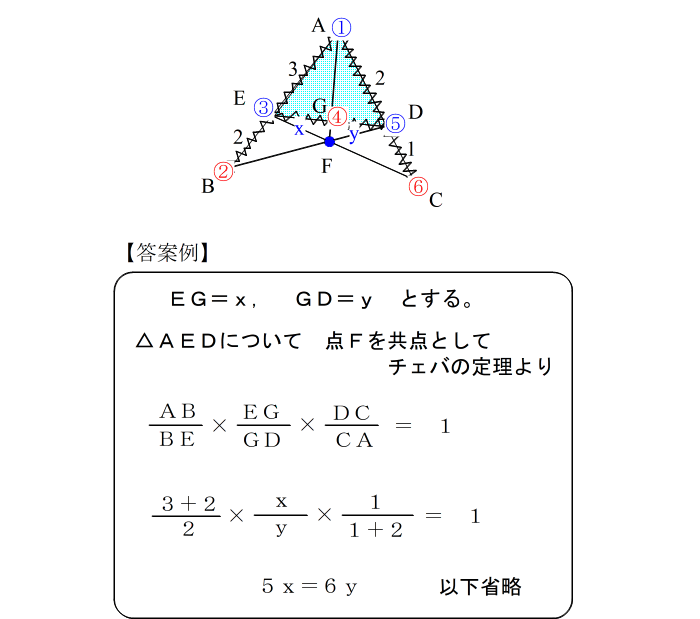
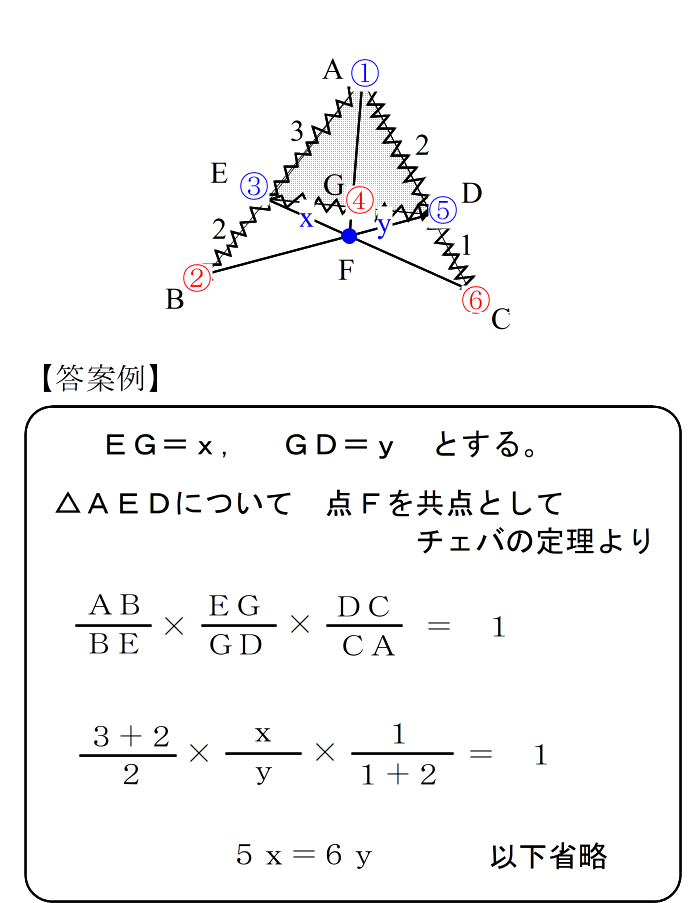
| 共点の存在が確認できたら (6)最後に メネラウスと同じ式に当てはめる。 |

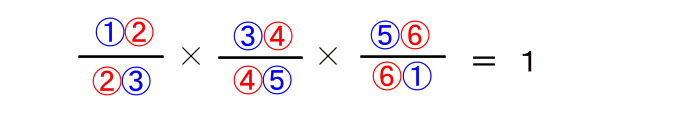
| 正式な答案も メネラウスとほぼ同じです。 |

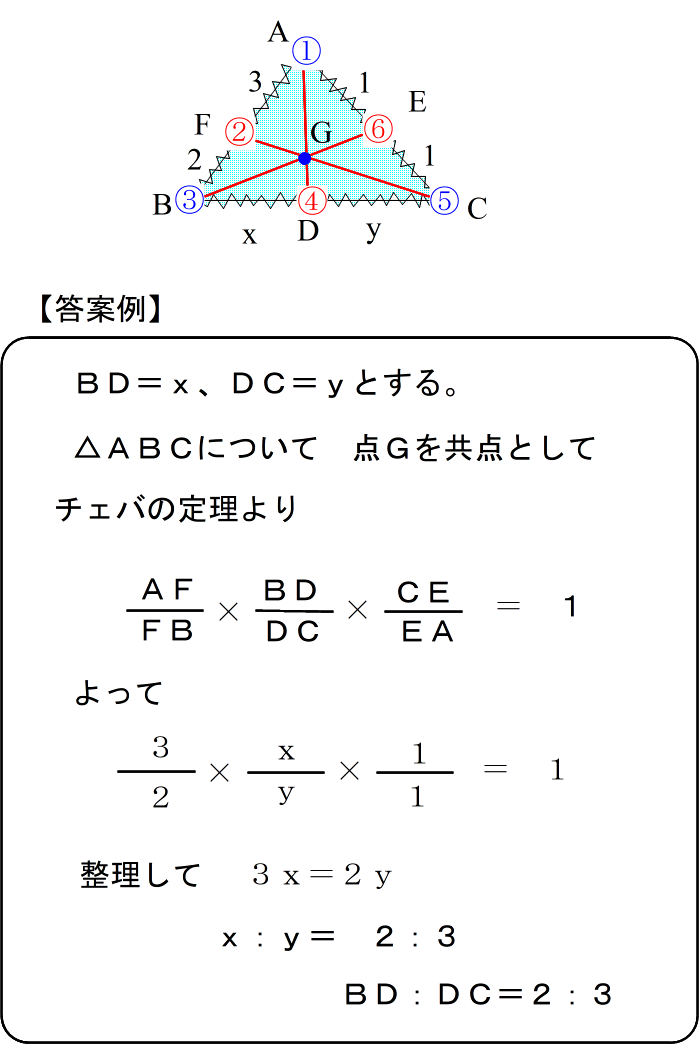
| 上の答案例で、「Gを共点として」とありますが、これは書かなくてもおそらく減点はされません。ただ書いた方が、わかりやすい答案になりますし、自分も納得しながら答案を書けると思います。 次は、教科書レベルを離れたちょっとわかりにくいパターンの問題です。 (時々出題されます。) 共点が三角形の外側に出たパターンの1つです。 |
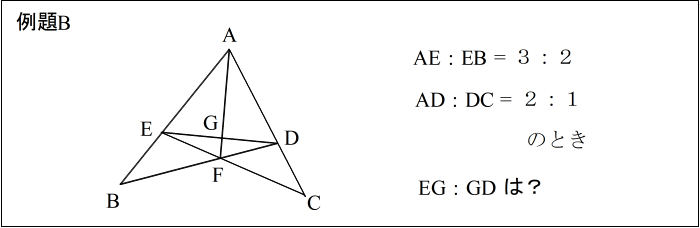
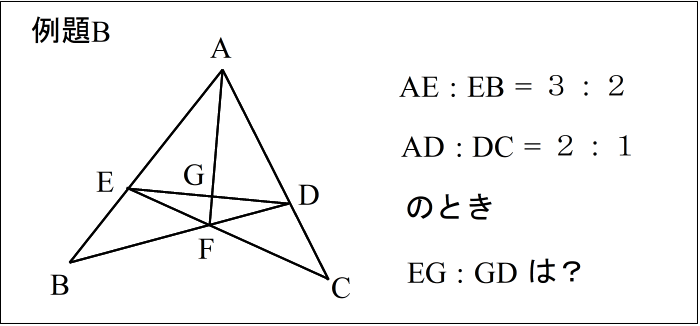
| 【作業】 手順通りに進めると下図のようになります。 |
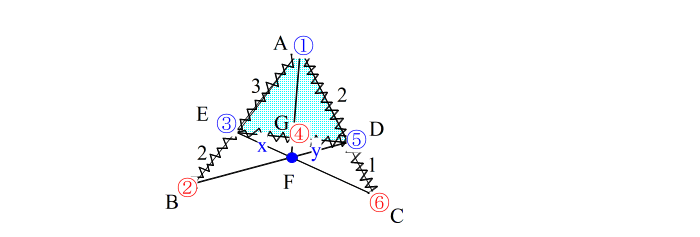
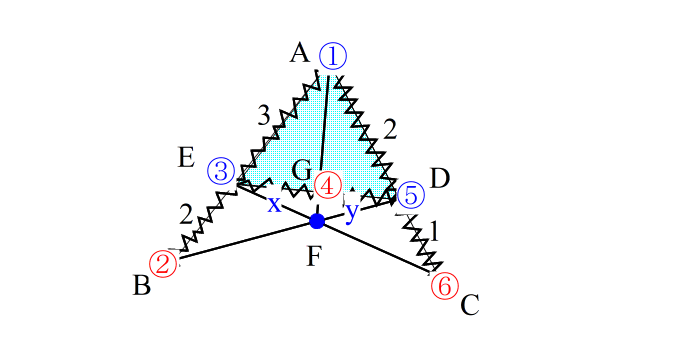
| ②④⑥は一直線上にないのでメネラウスは使えないが、 ①−④、 ③−⑥、 ⑤−② 3直線が一点Fで交わっているので、チェバが使える と判断する。 ※ この講座では上のような形のチェバを 「兜(かぶと)型のチェバ」 と呼ぶことにします。 |

 ・
・|
|
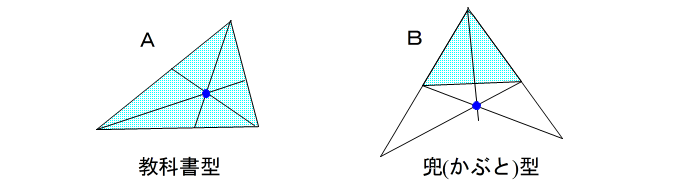
| 高校生が出会うチェバの定理の問題はこの2種類がほとんどです。 つまり A:共点が 三角形の内部にある場合 B:共点が 三角形の辺のすぐ外側にある場合 |
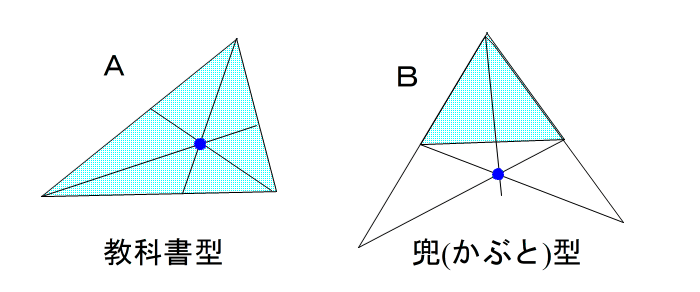
| しかし、個人的にもう1つだけやっておきたいので、おつきあい下さい。 |

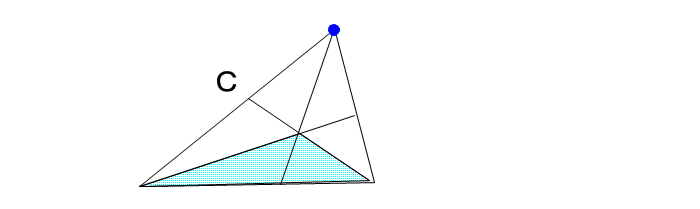
| C:共点が三角形の頂点の上方にある場合 です。 (「山上に月型」とでも名付けましょうか?) ※ちなみに、共点が三角形の外に出ると、分点の組み合わせは 「内・外・外」となります。 |
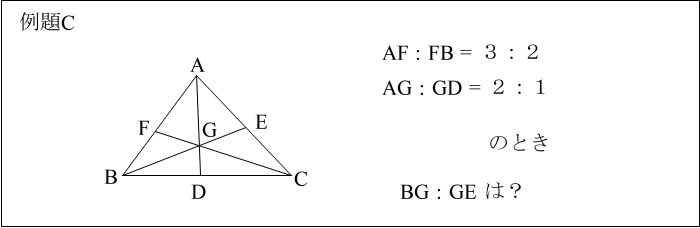
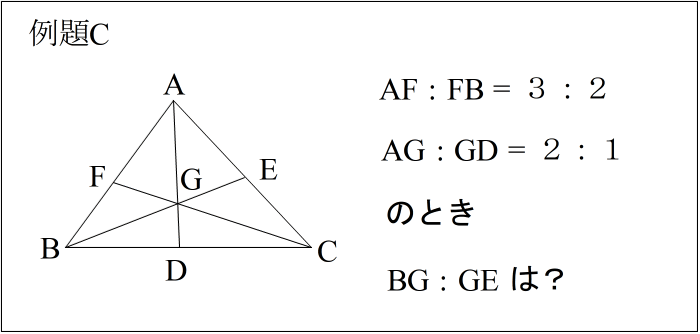
| 【作業】 手順通りに進めると下図のようになる。 |
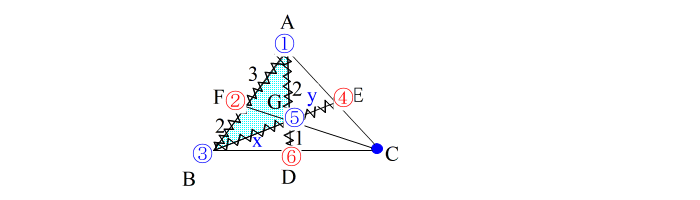
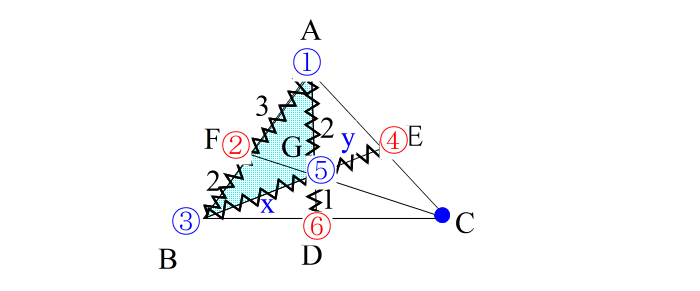
| ②④⑥は一直線上にないのでメネラウスは使えないが、 ①−④、 ③−⑥、 ⑤−② 3直線が一点Cで交わっているので、チェバが使える と判断する。 (今回は頂点⑤の上方に共点Cがあるパターン) |
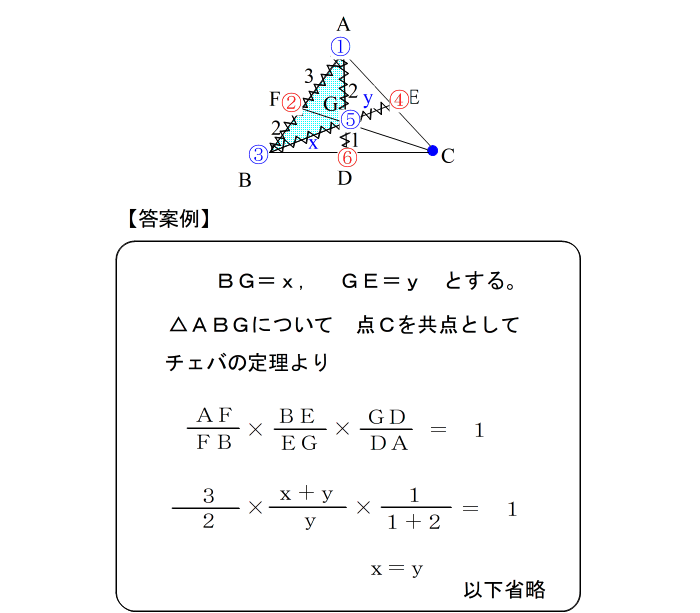
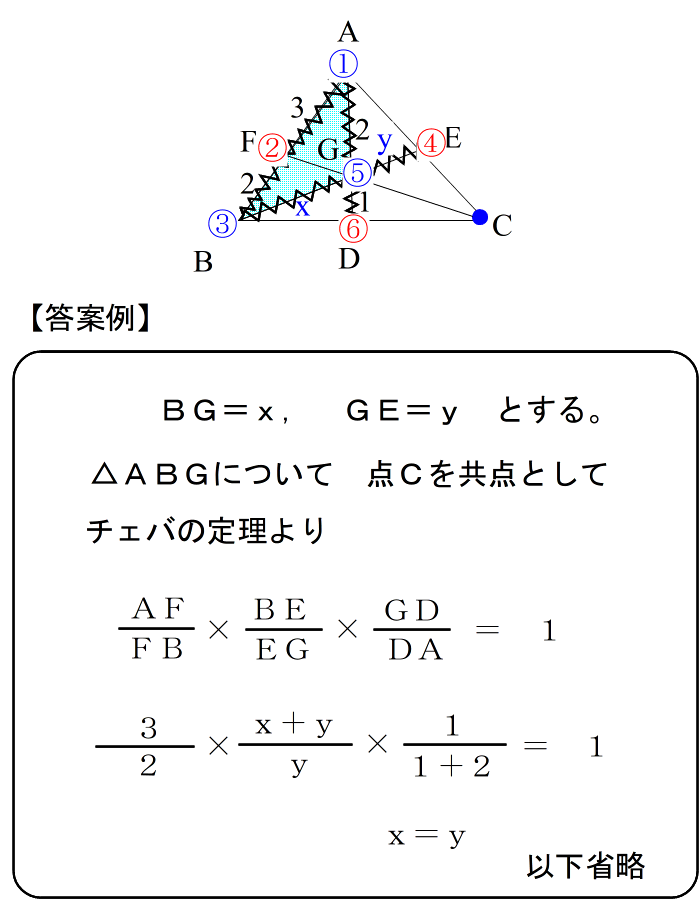
|
【解けないときの対処法】 (チェバ・メネラウス共通) (1) 三角形ができない場合 |
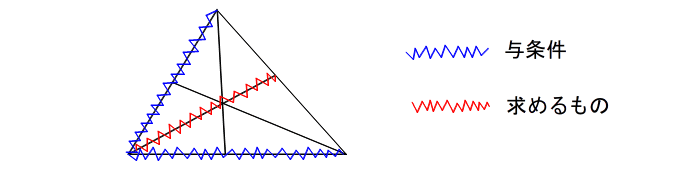
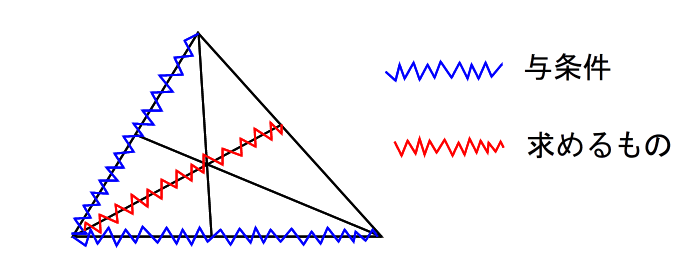
| 波線を引いてみたら上のようになった場合、三角形ができないので、メネラウスも、チェバも使えませんね。 ●まず、問題を読み間違ってないか確認しましょう。 間違いないときは、次のようにしましょう。 ●与条件を使って、一旦 別の辺の比を求めて、それを使って改めて別の式で求めましょう。 たとえば下のように チェバを使ってACを求めて、 |
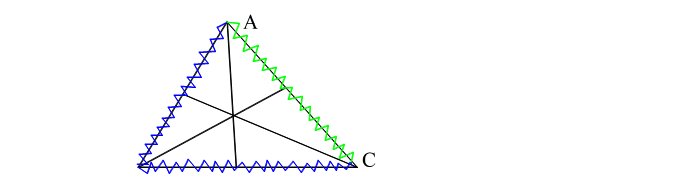
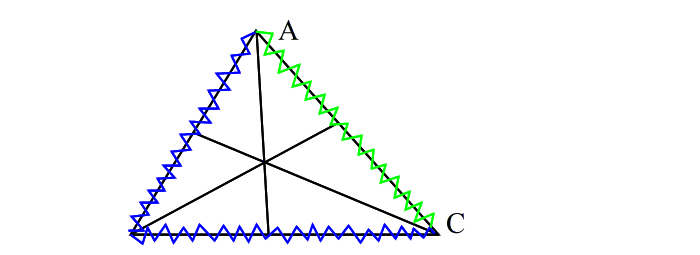
| 改めて、メネラウスで立式する。 |
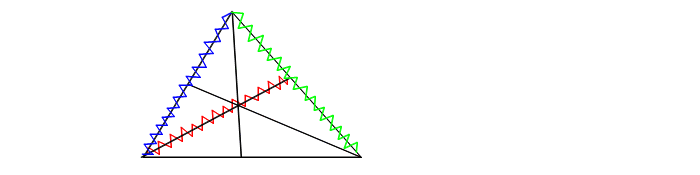
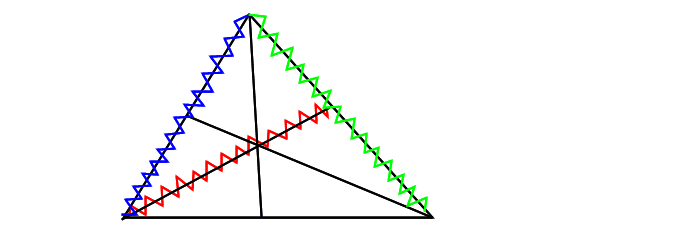
(2) 条件が多すぎる場合 わかっている比がたくさんありすぎて、どの波線で三角形を作れば良いかわからないことがあります。 そのときは ●適当に波線を選んで 三角形を作成してみます。 ( ただし、求める辺が三角形の辺に含まれるようにすること ) ●3つの分点②④⑥が直線になってさえいれば メネラウス。 三角形は複数パターン作成可能ですが、 メネラウスが使えるのであればどの三角形でやっても同じ答えになります。 どうしても②④⑥が直線にならなければ チェバができないか 確認します。 たとえば 作業を進めると 下のようになったとしましょう。 |
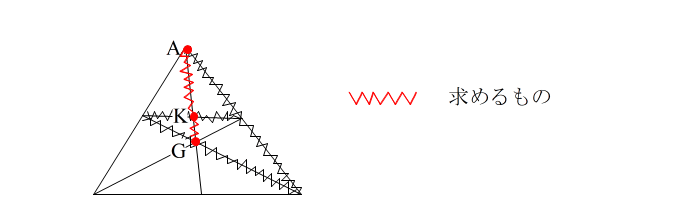
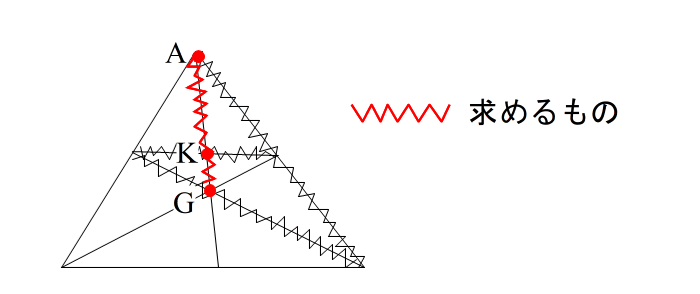
| ここで AK:KG がほしいとき A,K,Gの3点が 必ず三角形の頂点か分点になるように作るのがコツ。 この場合下のように メネラウスが 3種類できます。 |
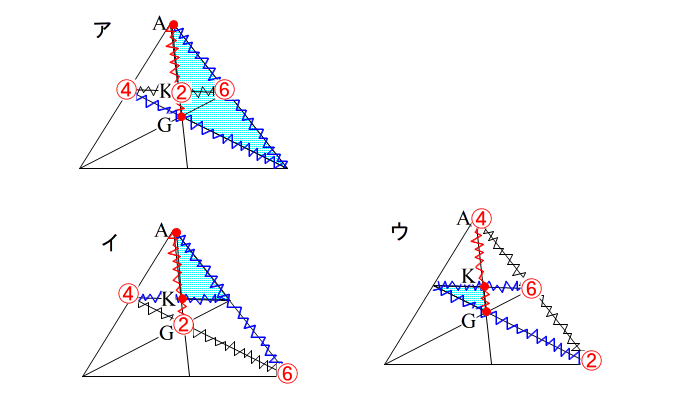
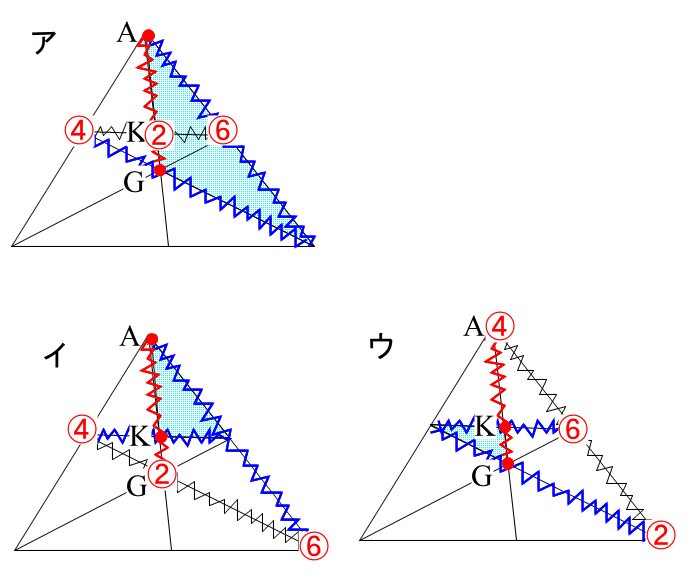
| ア、イ、ウ どれでやっても答えは同じです。 ※模範解答には ア(内・内・外)がたいてい使われます。 どうしても②④⑥が直線にならない場合は チェバを疑うか、(1)のように、一旦別の辺の比を求めてから、新たにトライする、ということになります。 特に兜(かぶと)型のチェバを使えるような図形では どこかでチェバを使うのだろうな、と考えた方が無難かもしれません。 |
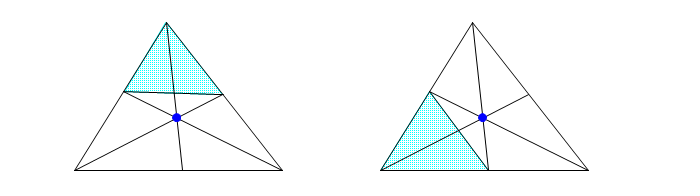
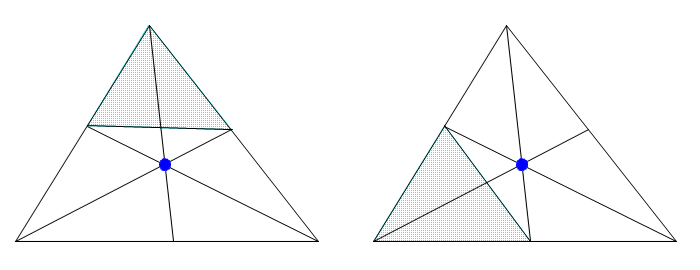
|
では最後に 練習問題をやってみて下さい。 チェバだけでなく、メネラウスも混ぜてありますから、どちらを使うべきか自分で判断して解いて下さい。 |
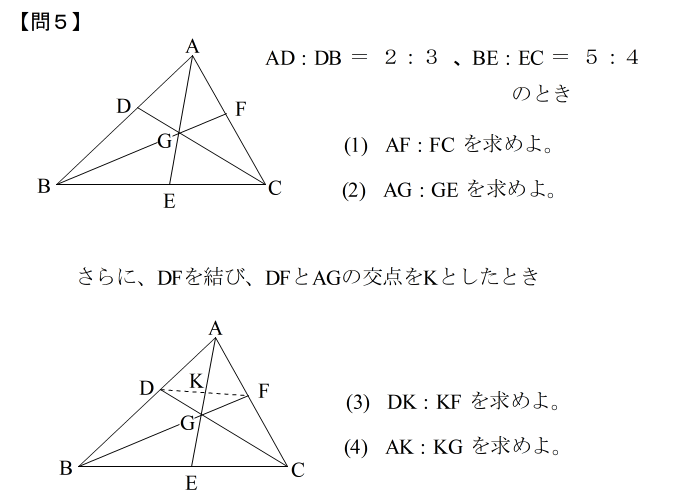
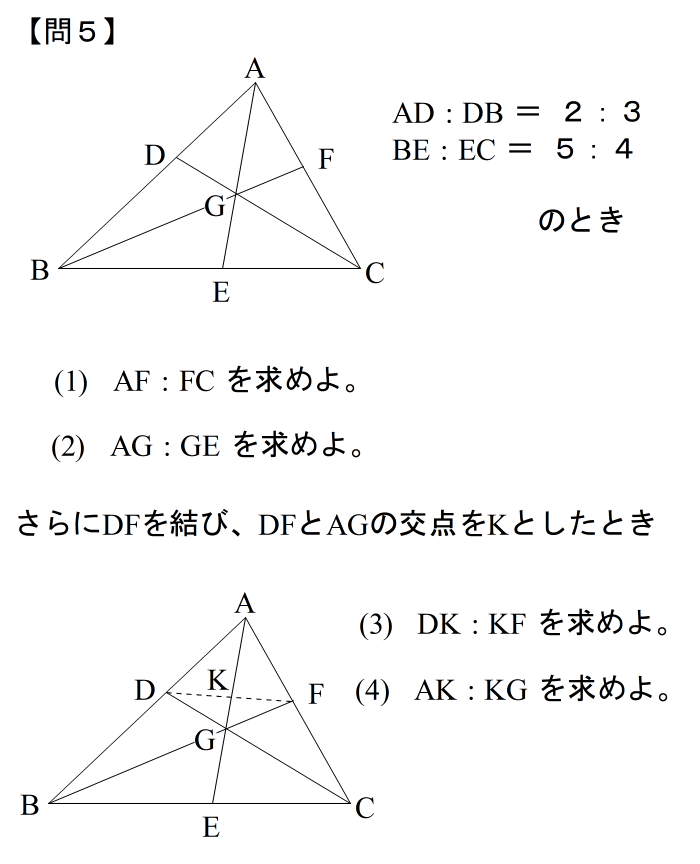
| 答えはこちら
|
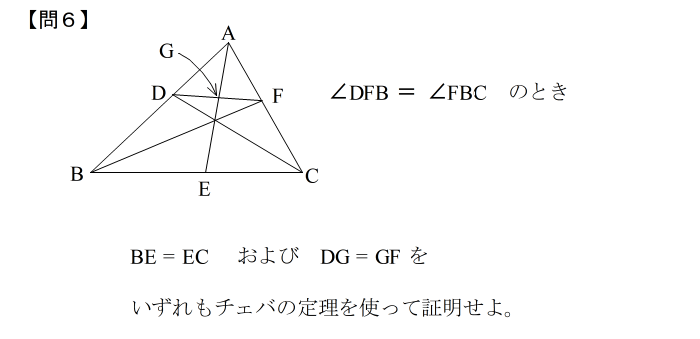
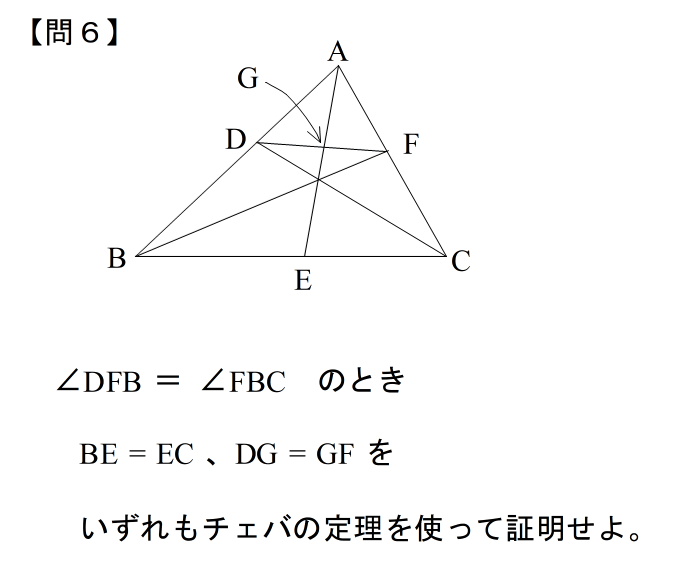
| 答えはこちら
|
| これで、メネラウスの定理、チェバの定理の講座は終わりです。 ご自分の教材に戻って、実践で試して下さい。 お願い:この講座は 2021年12月にリニューアルしました。 従って 誤字や内容のミスがあるかもしれません。 見つけた方は 下記の所までご一報下さい。 間違い指摘メールは こちらへ また、この講座をお読みになっての感想などございましたら是非お寄せ下さい。 ご感想メールは こちらへ |
| 塾長の 他の教材・講座 高校・世界史の教材 中学・歴史の教材 中学・地理の教材 |
| Copyright (C) since 2001 ARAKI, Shin-ichi All Right Reserved. |